Конвертер координат мск, ск-42/63, пз-90, wgs-84

ПЕРЕВОД ГЕОГРАФИЧЕСКИХ КООРДИНАТ В UTM(«Geo2utm», версия 1 от 05.07.2015, 01.00.00)

(In English: Program for convert of geographical coordinates to metrical (UTM))

Земля, как известно, имеет форму шара (не идеального, но в обиходе считается так). Но все карты земной поверхности всегда создаются на плоскости. Сферическую поверхность невозможно перенести на плоскость без искажений, поэтому издавна применяются различные системы перевода географических координат (широта и долгота) в прямоугольные, выраженные в метрах.

Существуют различные системы прямоугольных координат, но в международной геодезической практике наиболее популярна система UTM (от англ. Universal Transverse Mercator). В этой системе поверхность Земли делится на 60 зон по 6 градусов. Зоны «вертикальные», вытянутые в меридиональном направлении. В приполярной зоне погрешность этой системы слишком велика и там применяются другие варианты.

Перевод широты и долготы в метры UTM позволяет, в частности, проводить вычисления расстояний обычным сложением и вычитанием. Однако, надо учитывать, что координаты точек, расположенных в разных зонах, будут совпадать. Почему-то данная система не имеет выбранной нулевой точки координат и все расстояния отсчитываются фактически от начала зоны.

Из-за этой особенности прямой перевод широты и долготы в UTM не представляет особого труда, но вот обратный перевод (из UTM в географические координаты) требует обязательного указания номера зоны, где расположен объект. Впрочем, обратная задача гораздо меньше востребована…

На данной странице можно скачать бесплатную программу для перевода географических координат в UTM. Программа не требует установки и состоит из одного исполняемого файла размером 32768 байт.

Программа имеет три режима работы: ручной, файловый и буферный. В ручном режиме исходные значения широты и долготы вводятся вручную. Файловый режим позволяет обрабатывать блок исходных значений, считывая его из текстового файла, результат также помещается в файл. Буферный режим работает с данными из буфера обмена Windows.

В программе есть встроенная помощь, где подробно описана работа во всех режимах. Распространяется эта программа свободно для личного некоммерческого использования.

Необходимо отметить, что на данном сайте можно узнать также широту и долготу многих городов мира.

 СКАЧАТЬ «GEO2UTM»

Внимание! На отдельной странице можно выполнить онлайн преобразование географических координат в UTM, но у программы больше возможностей.

Использование

Из консоли

# если установлен через `pip install rosreestr2coord` или `python setup.py install`
rosreestr2coord -c 38:06:144003:4723
rosreestr2coord -l ./cadastral_numbers_list.txt
# запуск из директории проекта
python -m rosreestr2coord -c 38:06:144003:4723

Во время выполнения скрипта, в директории откуда был произведен запуск будут созданы файлы и папки.
Поэтому рекомендуется создать отдельную директорию для работы с приложением из консоли.

Опции:

• -h — справка
• -c — кадастровый номер
• -p — путь для промежуточных файлов
• -o — путь для полученного geojson файла
• -e — параметр, определяющий точность аппроксимации. Чем меньше, тем больше точек на полигоне:
• -t — тип площади:
  • 1 — Участки
  • 2 — Кварталы
  • 3 — Районы
  • 4 — Округа
  • 5 — ОКС
  • 6 — Тер. зоны; 7 — Границы; 9 — ГОК; 10 — ЗОУИТ; 12 — Лес; 13 — Красные линии; 15 — СРЗУ; 16 — ОЭЗ 16
• -l — пакетная загрузка из списка в текстовом файле ( )
• -d — визуализация распознанных точек (для режима —code)
• -r — не использовать кэширование
• -P — загрузка через прокси
• -C — экспортировать только центры участков
• -v — показать версию

Программно

from rosreestr2coord import Area

area = Area("38:06:144003:4723")
# аргументы
#   code='' - кадастровый номер участка
#   area_type=1 - тип площади
#   epsilon=5 - точность аппроксимации
#   media_path='' - путь для временных файлов
#   with_log=True - логирование
#   coord_out='EPSG:4326' - или EPSG:3857 (будет удалена в последующих версиях)
#   center_only=False - экспорт координат центров участка
#   with_proxy=False - запросы через прокси
#   use_cache=True - использовать кэширование запросов
area.to_geojson()
area.to_geojson_poly()
area.get_coord() # , , ], `area2_xyl`]
area.get_attrs()

Смена системы координат без перепроецирования в MapInfo Pro

Часто пользователи MapInfo Pro создают таблицы на территорию России, используя проекцию Гаусса-Крюгера (Пулково 1942). Однако, датум (номер 1001), используемый в данной системе координат, входящий в стандартную поставку MapInfo, предназначен для использования на территории Германии. В связи с этим, при передаче данных в другие ГИС или при переходе в другую координатную систему (например, ГСК-2011) происходит искажение координат объектов.

В этом случаем требуется сменить систему координат таблицы, при этом не трансформируя координаты.

Для того, чтобы изменить систему координат без перепроецирования необходимо сделать следующее:

1. экспортировать таблицу в mif/mid;
2. сменить строку системы координат в mif-файле используя любой текстовый редактор, например, Блокнот;
3. импортировать mif/mid в tab-файл.

Материал для статьи предоставлен Варущенко С.С. (ИПНГ РАН) и Макаровым С.Б. (МИИГАиК)

Вопросы и предложения по статье: support@mapinfo.ru

4.5. НАНЕСЕНИЕ НА КАРТУ ТОЧЕК ПО ЗАДАННЫМ ПРЯМОУГОЛЬНЫМ КООРДИНАТАМ

Чтобы нанести на карту точку по заданным прямоугольным координатам, поступают следующим образом: в записи координат находят двузначные числа, которыми сокращенно обозначены линии прямоугольной сетки. По первому числу находят на карте горизонтальную линию сетки, по второму – вертикальную. Их пересечение образует юго-западный угол квадрата, в котором лежит искомая точка. На восточной и западной сторонах квадрата откладывают от его южной стороны два равных отрезка, соответствующих в масштабе карты числу метров в абсциссе х. Концы отрезков соединяют прямой линией и на ней от западной стороны квадрата откладывают в масштабе карты отрезок, соответствующий числу метров в ординате; конец этого отрезка является искомой точкой.

Общая характеристика картографических данных объектов недвижимости

Под картографическими данными объектов недвижимости следует понимать их координаты. На обычной географической карте мира данные координаты обозначаются широтой и долготой. Однако в таких масштабах точно определить местоположение таких относительно мелких объектов, как дом или участок в несколько соток невозможно.

В этих целях ещё в Советском Союзе была разработана система координат СК63 (система координат 1963 года). Однако она не определяет индивидуальные координаты объектов, а лишь является способом их обозначения. На основе неё вся территория РФ была поделена на зоны, условно обозначенные латинскими буквами.

В целом, система использует три показателя:

• ширина и длина, обозначенные условно;
• высота – согласно Балтийской системе высот.

Однако основные инструменты обозначения остались неизменными. За основу берётся масштаб, равный 1:100 000.

Масштаб может быть увеличен или уменьшен в зависимости от насыщенности местности объектами недвижимости.

4.6. ВЫЧИСЛЕНИЕ ПЛОСКИХ ПРЯМОУГОЛЬНЫХ КООРДИНАТ ГАУССА ПО ГЕОГРАФИЧЕСКИМ КООРДИНАТАМ

Плоские прямоугольные координаты Гаусса х и у весьма сложно связаны с географическими координатами φ (широта) и λ (долгота) точек земной поверхности. Предположим, что некоторая точка А имеет географические координаты φ и λ. Поскольку разность долгот граничных меридианов зоны равна 6°, то соответственно для каждой из зон можно получить долготы крайних меридианов: 1-я зона (0° – 6°), 2-я зона (6° – 12°), 3-я зона (12° – 18°) и т.д. Таким образом, по географической долготе точки А можно определить номер зоны, в которой эта точка находится. При этом долгота λос осевого меридиана зоны определится по формуле λ _ос = (6°n – 3°), в которой n – номер зоны.

Для определения плоских прямоугольных координат х и у по географическим координатам φ и λ воспользуемся формулами, выведенными для референц-эллипсоида Красовского (референц-эллипсоид – фигура, максимально приближенная к фигуре Земли в той ее части, на которой находится данное государство, либо группа государств):

По формуле (4.1) значение координаты у(l) получают относительно осевого меридиана зоны, т.е. оно может получиться со знаками «плюс» для восточной части зоны или «минус» – для западной части зоны. Для записи координаты y в зональной системе координат необходимо вычислить расстояние до точки от осевого меридиана зоны, отнесенного западнее на 500 км (у‘в таблице), а впереди полученного значения приписать номер зоны. Например, получено значение у(l) = –303678,774 м в 47 зоне. Тогда у = 47 (500000,000 – 303678,774) = 47196321,226 м. Для вычислений используем электронные таблицы MicrosoftXL.

Пример. Вычислить прямоугольные координаты точки, имеющей географические координаты: φ = 47º02’15,0543″ с.ш.; λ = 65º01’38,2456″ в.д.

В таблицу MicrosoftXL вводим исходные данные и формулы (таб. 4.1).

Для чего нужен перевод?

Необходимость перевода координат объекта недвижимости может понадобиться в разных жизненных ситуациях. Это может быть как определение границ участка, так и расположение будущих зданий и сооружений на участке земли.

Вот классический пример.: Строительная компания при оформлении  разрешительных документов для строительства предоставила в государственный орган карту местности с указанием на границы будущей постройки и затрагиваемые смежные участки земли. При проведении проверки со стороны госоргана выяснилось, что в части участка имеется исторический памятник – древнее захоронение. При выдаче разрешения на строительство на карте, как правило – географической, указывается точки, которые нельзя затрагивать. Возникает необходимость перевода указанных координат на карту местности, по которой рассчитывались границы строительства.

Стоит отметить, что даже наличие специальных знаний и навыков не могут гарантировать точность расчётов, так как карты представляют собой плоскость, тогда как реальный объект недвижимости располагается на трёхмерной поверхности. Именно данная нелинейность реальных показателей являются причиной ошибок в несколько метров, порой даже километров при определении местоположения таких объектов на карте.

2.2 Сферическая система координат

Телом отсчета для сферической системы координат является сфера с радиусом
. Начало этой системы координат совмещают с центром сферы. Координатами
являются геоцентрическая широта , долгота и радиус-вектор . Широтой
называется угол между радиусом-вектором и плоскостью экватора. Долгота есть
угол между плоскостью, проходящей через заданную точку и осью вращения
(плоскость меридиана) и плоскостью меридиана, принятого в качестве нулевого.
Связь между сферической системой и глобальной декартовой определяется
формулами

(2.1)

В том случае, когда широта определяется как угол между плоскостью экватора и
отвесной линией, сферическая система координат называется астрономической. Широта и долгота, определенные
в этой системе мы будем обозначать через и .

2.4 Эллипсоидальная система координат

Рассмотрим еще одну систему координат, имеющую приложение в теории
гравитационного потенциала:

Эти формулы содержат не три, а четыре переменные величины. Четвертая
переменная устанавливает семейство координатных поверхностей — эллипсоидов.
Убедимся в этом. Проделаем простые преобразования:

Разделив первое уравнение на
а второе — на

, получим

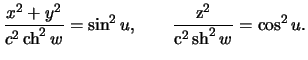
Очевидно, что при
получим уравнение эллипсоида вращения

Поскольку
,
имеем
, отсюда
параметр имеет простой физический смысл: он равен половине межфокусного
расстояния. Понятно, что изменяя при условии
,
получим семейство софокусных
эллипсоидов, играющих важную роль в теории потенциала фигур равновесия
Построим теперь семейство координатных поверхностей
.
Проделаем очевидные
преобразования

меняя , получим семейство однополостных гиперболоидов вращения. Обозначив
, , получим уравнение гиперболоида в общепринятой форме.

Разделив у на х, получим

. Изменяя , получим семейство плоскостей,
проходящее через ось Оz. Все
три семейства поверхностей образуют взаимно ортогональную систему.

Лекция 1. Теория фигуры земли
| Оглавление |
Лекция 3. Теория потенциала >>

Способы перевода

Перевести геодезические координаты объекта недвижимости в географические на сегодняшний день представляется задачей сложной. Всё дело заключается в закрытости подробной информации и нелинейности картографических данных, из-за чего в итоге расчётов могут возникнуть сдвиги от нескольких метров до нескольких километров.

Однако разработано множество программ, которые облегчают процесс проведения пересчёта. Одной из них является GPSMapEdit. К сожалению, российских программ не существует, и для расчёта необходимо самостоятельно вводить данные ключевых точек (ключ расчёта), причём делать это нужно очень точно. Но даже в этом случае сдвигов в несколько метров не избежать, так как ключи большинства регионов до сих пор не доработаны.

К  примеру, переложение данных из геодезической карты в географическую и наоборот по ключам МСК – 50 (Москва) зона 2 получается точным, чего не скажешь обо всех регионах.

Другим способом является осуществление расчётов на специальных сайтах, где установлены геокалькуляторы с учётом данный российских топографических карт. К примеру:

1. latlong.ru – сайт довольно популярный и по основным регионам (Москва, Санкт-Петербург) выдаёт точные результаты. Но всё зависит от вводных данных. Нужно просто ввести имеющие координаты по ГСК-2011 (Основа МСК) или координаты по GPS. Однако возможно сдвиги в несколько километров.
2. www.the-mostly.ru – простой и удобный калькулятор для перевода картографических координат в виде десятичных дробей в стандартные показатели широты и долготы в градусах, минутах, секундах. Точная ссылка на вкладку: http://the-mostly.ru/konverter_geograficheskikh_koordinat.html.

Поискав на просторах интернета, можно найти десятки подобных сайтов, но никто не гарантирует точность расчётов и уж тем более не обеспечивает правовой статус перевода. Ведь в основном перевод может пригодиться для представления в государственные органы или же исполнения указаний органов власти.

Под ответом органа ставиться печать государственного образца, которая подстрахует от ответственности в случае чего.

Двусторонний спутниковый Интернет

Что такое географические координаты?

Географические координаты определяют положение точки на земной поверхности. Географические координаты строятся по принципу сферических и состоят из широты и долготы.

Широта — угол между местным направлением зенита и плоскостью экватора, отсчитываемый от 0° до 90° в обе стороны от экватора. Географическую широту точек, лежащих в северном полушарии, (северную широту) принято считать положительной, широту точек в южном полушарии — отрицательной. О широтах, близких к полюсам, принято говорить как о высоких, а о близких к экватору — как о низких.

Долгота — угол между плоскостью меридиана, проходящего через данную точку, и плоскостью начального нулевого меридиана, от которого ведётся отсчёт долготы. Долготы от 0° до 180° к востоку от нулевого меридиана называют восточными, к западу — западными. Восточные долготы принято считать положительными, западные — отрицательными.

Формат записи географических координат

Географические координаты одной точки могут быть выражены в разных форматах. В зависимости от того, представлены минуты и секунды как значения от 0 до 60 или от 0 до 100 (десятичные доли).

Формат координат обычно записывают следующим образом: DD — градусы, MM — минуты, SS — секунды, если минуты и секунды представлены как десятичные доли, то пишут просто DD.DDDD. Например:

1. DD MM SS: 50° 40′ 45» в.д., 40 50′ 30» с.ш. — градусы, минуты, секунды
2. DD MM.MM: 50° 40.75′ в.д., 40 50.5′ с.ш. — градусы, десятичные минуты
3. DD.DDDDD: 50.67916 в.д., 40.841666 с.ш. — десятичные градусы

Для чего нужно знать координаты своего дома

Зачастую дома в дачных поселках и многих деревнях не имеют четкой навигации состоящей из вывесок с названиями улиц и нумерации домов или даже дома имея вывески с номерами могут быть раскиданы по всему поселку в случайном порядке (исторически сложившемуся по мере застройки поселка). Бывают случаи, что с навигацией в населенном пункте все хорошо, но не во всех автомобильных GPS-навигаторах такой дом или улица находится. Жителям таких домов приходится долго и, как правило, запутанно объяснять как до них добраться используя разные ориентиры. В таком случае проще дать координаты дома, ведь любой автомобильный навигатор может проложить путь по координатам.

Для проработки технической возможности подключения Интернета в загородном доме мы также просим своих заказчиков предоставить координаты дома, особенно в том случае если ни на одном из картографических онлайн-сервисов он не находится по адресу.

Определение координат с помощью картографических онлайн-сервисов

В настоящее время самыми известными картографическими онлайн-сервисами с функцией поиска являются карты Google и Yandex. Рассмотрим, как можно определить географические координаты по карте или снимку со спутника в сервисе Maps:

1. Откройте Карты Google https://maps.google.ru

2. Найдите на карте точное место. Для этого карту можно двигать мышью, приближать и удалять прокручивая колесико мыши. Также можно найти нужный населенный пункт с помощью поиска по названию используя населенный пункт, улицу и дом. Чтобы максимально точно найти место дома переключайтесь между режимами отображения: Карта, Гибрид или Спутник.

3. Щелкните правой кнопкой мыши по нужному месту на карте и выберите из открывшегося меню пункт “Что тут находится?”. На карте появится маркер в виде зеленой стрелки. Повторите операцию, если маркер установился неточно.

4. При наведении мыши на зеленую стрелку появятся географические координаты места, также они появятся и в строке поиска откуда их можно скопировать в буфер обмена.

Рис. 1. Определение координат места по указателю на карте Google

Теперь рассмотрим как можно определить географические координаты по карте или снимку со спутника в сервисе Яндекс.Карты:

Для поиска места применим тот же алгоритм, что и для поиска на картах Google. Откройте Яндекс.Карты: https://maps.yandex.ru. Для получения координат на Яндекс-карте используется инструмент «Получить информацию» (кнопка со стрелкой и знаком вопроса, в левой верхней части карты). При щелчке этим инструментом по карте на ней появляется маркер, а в строке поиска отображаются координаты.

Рис. 2. Определение координат места по указателю на Яндекс-карте

На картах поисковых систем по умолчанию показываются координаты в градусах с десятичной дробью со знаками «-» для отрицательной долготы. На картах Google и картах Яндекс вначале широта, затем долгота (до октября 2012 на картах Яндекс был принят обратный порядок: сначала долгота, потом широта).

Настройка MapInfo Pro

В MapInfo Pro параметры систем координат задаются в файле MapInfow.prj. Файл проекций MapInfow.prj, находится в той же папке, где установлена MapInfo Pro, а начиная с 17 версии в подпапке с языком программы (ru – для русского). Следует отметить, что чаще всего, программа MapInfo Pro установлена в папке «Program Files», что требует прав Администратора для редактирования этого файла. Для редактирования этого файла можно использовать любой текстовый редактор, например, Блокнот. 

Каждая строка файла MapInfow.prj определяет координатную систему или категорию.

Координатная система задаётся строкой:

«Название КС», Тип_проекции, Датум, , … параметры проекции

Название КС: название, которое будет появляться в списке проекций.

Тип_проекции: номер, определяющий уравнения, которыми задаются координатная система.

Датум: номер, определяющий параметры датума.

Чтобы создать координатную систему с собственным датумом, следует вместо номера датума использовать номер 9999, после которого должны быть перечислены значения в следующем порядке:

9999, Номер_Эллипсоида, ΔX, ΔY, ΔZ, ω_x, ω_y, ω_z, m, Нулевой_Меридиан

Например, для проекции Долгота/Широта СК-95:

«Долгота/Широта (СК-95)», 1, 9999, 3, 24.47, -130.89, -81.56, 0, 0, -0.13, -0.22, 0

Цифра «1» после названия системы координат означает, что используется проекция Долгота/Широта.

Для проекции Гаусса-Крюгера в СК-42:

«ГК Зона 7 (СК-42)», 8, 9999, 3, 23.57, -140.95, -79.8, 0, -0.35, -0.79, -0.22, 0, 7, 39, 0, 1, 7500000, 0

Цифра «8» после названия системы координат означает, что используется поперечная проекция Меркатора (Гаусса-Крюгера), значения  — «7, 39, 0, 1, 7500000, 0» являются  параметрами проекции Гаусса-Крюгера для 7 зоны. Значения для других зон можно взять из файла MapInfow.prj для «— Гаусса-Крюгера (Пулково 1942) —«

Категории проекций используются для группировки систем координат. Чтобы задать свою категорию проекций требуется указать в отдельной строке:

— Название категории —

Координатные системы, определённые после этой строки будут помещены в эту категорию.

Подробнее о задании собственных систем координат можно узнать в руководстве пользователя (MapInfoProUserGuide.pdf), включённом в поставку MapInfo Pro.

2.3 Геодезическая система координат

С геодезической системой координат связывают понятия геодезической
широты, долготы и высоты. Геодезическая широта В есть угол, под которым
пересекается нормаль к поверхности эллипсоида с плоскостью экватора. Долгота
— двугранный угол между плоскостью нулевого меридиана и плоскостью
меридиана, проходящего через заданную точку.

Геодезические широта и долгота отличаются от соответствующих астрономических
координат, связанных с отвесной линией, так как отвесная линия не совпадает
с нормалью к эллипсоиду. Отклонение отвесной линии можно спроецировать на
две плоскости: плоскость меридиана и плоскость первого вертикала. Нетрудно
понять, что обе эти составляющие можно определить через разности между
астрономическими и геодезическими координатами

(2.2)

Отклонения отвесной линии составляют, как правило, первые несколько секунд
дуги.

Заметим, что геодезическая и геоцентрическая долготы совпадают. Обе они
определены как двугранный угол между плоскостью нулевого меридиана и
плоскостью, содержащей ось вращения и заданную точку. Геоцентрическая же
широта отличается от геодезической.

Рассмотрим точку , лежащую вне ОЗЭ. Опустим из этой точки перпендикуляр на
поверхность эллипсоида и продолжим его до пересечения с экваториальной
плоскостью ().
Проекцию точки на поверхность эллипсоида обозначим через
Тогда отрезок PQ есть геодезическая высота точки .
Угол, под которым упомянутый
перпендикуляр пересекает плоскость экватора, есть геодезическая широта . Она
относится как к точке , так и к точке . Геоцентрические широты этих двух
точек, как видно из рисунка, различаются. Геоцентрическая широта точки угол
между радиус-вектором этой точки и плоскостью экватора.

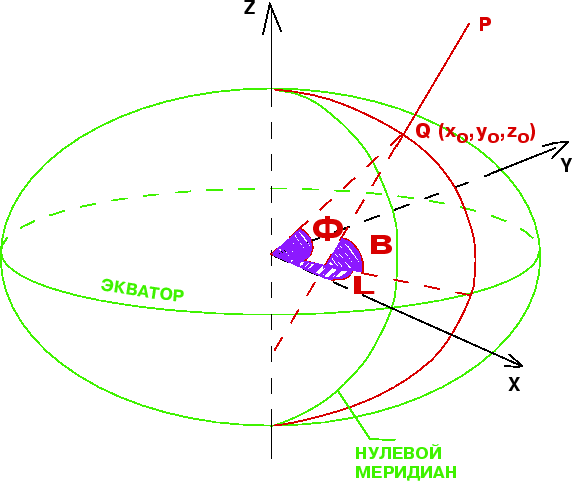Рис. 2.

Установим связь между координатами точки , сжатием эллипсоида и
широтами и . Поскольку точка лежит на поверхности эллипсоида, то ее
прямоугольные координаты
подчиняются уравнению
эллипсоида вращения:
. Рассмотрим сечение .
Тогда, как легко
видеть,
. Чтобы
определить , нужно найти угловой коэффициент нормали в точке .
Уравнение
нормали к кривой в точке
имеет вид

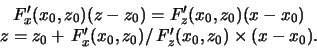(2.3)

У нас
,
поэтому
,

,

Следовательно,

Определим отличие геоцентрической широты от геодезической .
Имеем очевидные равенства

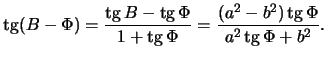(2.4)

Второй эксцентриситет эллипса, как мы знаем, определяется следующим образом

, поэтому

Для Земли второй эксцентриситет мал, поэтому, пренебрегая малыми второго
порядка относительно сжатия, получим
. Можно
также считать, что

Учитывая сказанное, получим

Наибольшее отличие геодезической широты от геоцентрической достигается на
широте 45° и составляет
.

Связь глобальных декартовых координат с геоцентрическими определяется
формулами (). Определим теперь формулы, связывающие декартовы
координаты с
геодезическими. Это означает, что бы должны определить координаты точки
через параметры эллипсоида и геодезические широту и долготу.

Поскольку
, для определения координат , , точки
достаточно, для начала,
определить только координаты и ,
то есть все рассуждения проводить только
для сечения . Обратимся к .

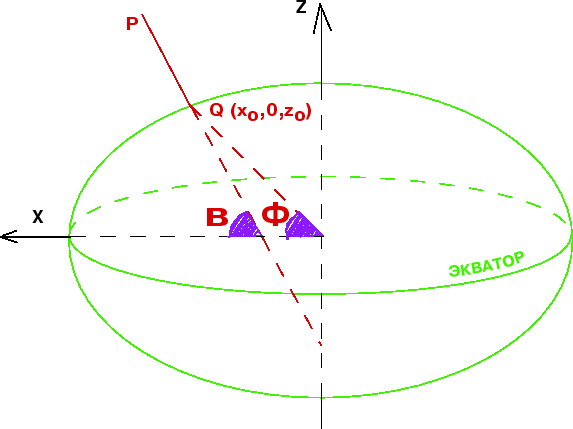Рис. 3.

Определим прямоугольные координаты точки , расположенной на высоте Н над
поверхностью эллипсоида. Сначала определим координаты проекции точки на
поверхность эллипсоида (точка ). Ее координаты в сечении Охz равны

Индексом «0» мы отметили принадлежность координат к точке, лежащей на
поверхности эллипсоида. Как мы видели

поэтому

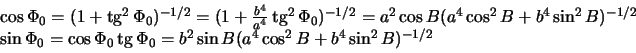
Остается определить радиус-вектор точки .
Воспользуемся уравнением эллипса
и выполним необходимые преобразования.

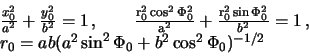(2.5)

Выразим
и
через и
, для чего
воспользуемся приведенными выше формулами. Определим радиус-вектор точки

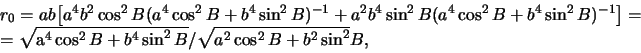
следовательно,

(2.6)

Обозначим

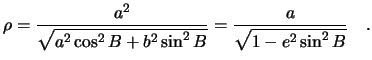(2.7)

Теперь

(2.8)

Для произвольного сечения, проходящего через ось вращения ,
будем иметь

(2.9)

Теперь поднимем точку на высоту Н и совместим ее с точкой .
Прямоугольные координаты изменятся на

(2.10)

Окончательно, теперь формулы для пересчета геодезических координат и Н в
прямоугольные примут вид

(2.11)

Здесь , определенный формулой () имеет простой геометрический смысл:
он равен отрезку нормали, проходящей через точку , от этой точки до точки
пересечения ее с осью вращения эллипсоида. Справедливость этого утверждения
предлагается доказать самостоятельно.

Лекция 2. Геодезические системы координат

Сферическая система. Широта долгота и радиус-вектор.
Система координат, построенная на эллипсоиде.
Геодезические координаты: широта, долгота и высота.
Связь между сферической, геодезической и декартовой
системами координат.

Геодезические задачи решают на плоскости, если размеры площади невелики. Если
исследуемая часть поверхности занимает несколько градусов широты или
долготы, то необходимо учитывать и кривизну поверхности. В этом случае часто
подходит и шар. Для решения глобальных задач, в том числе и задач по
космической геодезии в качестве тела отсчета берут эллипсоид вращения. В
частности на эллипсоиде решают следующие задачи:

—

Уточнение формы и размеров общего земного эллипсоида (ОЗЭ).

—

Перенос направлений и расстояний с физической поверхности на эллипсоид.

—

Определение координат точек на поверхности референц-эллипсоида.

—

Определение расстояний между точками с заданными координатами.

—

Уточнение координат по мере уточнения элементов эллипсоида.

Что представляют собой прямоугольные координаты

Основа проекций эллипса на плоскость — что по Гауссу-Крюгеру, что по системе UTM — это принцип прямолинейных исчислений Декарта.

Система плоских прямоугольных координат

Величины имеют как плюсовое значение, так и минусовое, что зависит от положения относительно квадранта:

Для проекции Гаусса-Крюгера отображаемая на карте территория разделена на 60 зон, где расстояние между меридианами приравнено к 6º. Отсчет идет от Гринвича к востоку и к экватору на север. За коэффициент масштаба взята единица. Точкой отсчета выступает пересечение выбранного меридиана с экватором.

Для разработанной американцами системы UTM характерны аналогичные деления на 60 зон, но расчетный меридиан иной — первая по нумерации зона ведет начало от меридиана 177º западной долготы. Также отличия касаются масштабного коэффициента — он равен 0,9996. В системе UTM отсутствуют отрицательные значения — для этого к западной абсциссе приплюсовывают 500 километров, а к южной ординате — 10 тысяч километров.

Общая характеристика картографических данных объектов недвижимости

Под картографическими данными объектов недвижимости следует понимать их координаты. На обычной географической карте мира данные координаты обозначаются широтой и долготой. Однако в таких масштабах точно определить местоположение таких относительно мелких объектов, как дом или участок в несколько соток невозможно.

В этих целях ещё в Советском Союзе была разработана система координат СК63 (система координат 1963 года). Однако она не определяет индивидуальные координаты объектов, а лишь является способом их обозначения. На основе неё вся территория РФ была поделена на зоны, условно обозначенные латинскими буквами.

В целом, система использует три показателя:

• ширина и длина, обозначенные условно;
• высота – согласно Балтийской системе высот.

Однако основные инструменты обозначения остались неизменными. За основу берётся масштаб, равный 1:100 000.

Масштаб может быть увеличен или уменьшен в зависимости от насыщенности местности объектами недвижимости.

Алгоритмы перевода географических координат в прямоугольные

Для быстрого пересчета географических координат в прямолинейные и обратно действуют особые алгоритмы, которые стали основой автоматических программ по такому сервису. Разработаны также онлайн конвертеры, пересчитывающие как координаты Гаусса — Крюгера, так и UTM, когда градус нахождения объекта, даже его минута и секунда превращаются в точные метры — и наоборот, когда метры трансформируются в градусы.

В программу либо конвертер вводятся параметры широты с долготой, на которых расположен наш объект, а на выходе имеем величины x (горизонтальный параметр) и y (вертикальный параметр). Аналогично делается обратный перевод.

В спутниковой навигации ГЛОНАСС и GPS действует постоянное отслеживание координат любого заданного формата. Можно задать величины, чтобы показывалась широта и долгота, а одновременно отображались метры либо километры.

Преобразования координат

Чтобы определить ширину и долготу – координаты местоположения на Земле, как минимум нужно иметь возможность видеть звезды или Солнце, иметь секстан и часы, показывающие время на меридиане GMT. Можно определить широту из угла между небесным телом и горизонтом, а долготу можно вычислить из вращения Земли. Эта статья не погружается в подобные подробности, но в разделе о них можно узнать больше. Вместо этого, предположим, что у нас уже есть координаты в формате DD, DMS или UTM.

Преобразование десятичных градусов в градусы/минуты/секунды и обратно

Крайне просто преобразовать координаты из формата DD в DMS. Ниже приведена формула для подобного преобразования:

DD: dd.ff
DMS: dd mm ss

dd=dd
mm.gg=60*ff
ss=60*gg

В этом примере – это дробная часть вычисления. Отрицательная широта означает местоположение в южном полушарии (S), а отрицательная долгота – в западном полушарии (W). Например, предположим, что имеются координаты в формате DD – 61.44, 25.40. Их можно преобразовать следующим образом:

lat dd=61
lat mm.gg=60*0.44=26.4
lat ss=60*0.4=24

Далее:

lon dd=25
lon mm.gg=60*0.40=24.0
lon ss=60*0.0=0

Таким образом, в формате DMS получаем следующие координаты – 61°26’24”N 25°24’00”E.

Ниже приведена формула для перехода от DMS к DD:

DD: dd.ff
DMS: dd mm ss

dd.ff=dd + mm/60 + ss/3600

Напомним, что места, расположенные в южном полушарии (S), имеют отрицательную широту, а места в западном полушарии (W) имеют отрицательную долготу.

Теперь выполним преобразование DMS координат 47°02’24”S, 73°28’48”W в формат DD:

lat dd.ff= - (47 + 2/60 + 24/3600 )=-47.04
lon dd.ff= - (73 + 28/60 + 48/3600)=-73.48

Таким образом, координаты в DD равны -47.04, -73.48.

Преобразование долготы/широты в UTM и обратно

В отличие от десятичных координат, которые можно определить с помощью хронометра и часов, координаты UTM невозможно определить без помощи вычислений. Хотя эти вычисления ничто иное, как простая тригонометрия и алгебра, формулы у них достаточно сложные. Если ознакомиться со статьей “The Universal Grids: Universal Transverse Mercator (UTM) and Universal Polar Stereographic (UPS)” (ссылка на неё приведена в разделе ), то станет понятно, что я имею ввиду.

Формулы для преобразования UTM здесь не приводятся, но исходный код в следующем разделе немного освещает эту проблему, а в разделе есть ссылки на дополнительную информацию.

Журнал

• 09.07.2020 — v.4.0.10
  • Исправлен экспорт в KML #36.
  • Добавлена опция консоли для вывода текущей версии библиотеки
• 28.05.2020 — v.4.0.9

  Исправлена проблема с путями в Windows #34.

• 14.05.2020 — v.4.0.8 by alexandervlpl

  Оптимизировать склеивание тайлов #30.

• 12.05.2020 — v.4.0.7
  • Исправление экспорта мультиполигональной геометрии.
  • Экспорт в KML #31.
• 10.05.2020 — v.4.0.6

  Обработка запросов с ошибоками, исправление кэширования.

• 01.05.2020 — v.4.0.5
  • Загрузка ЗОУИТ (-t 10).
  • Добавлен файл привязки к получаемому растру.
• 21.04.2020 — v.4.0.4 by magican
  • небольшой рефакторинг — подготовка к type и pep тестам.
  • добавлен poetry.
  • добавлен Makefile.
  • добавлены тесты (pytest).
• 08.04.2020 — v.4.0.0
  • Координаты всегда в WGS84.
  • Всегда добавляются атрибуты.
  • Каталог заменен на кэширование запростов.
  • Из проекта удалён GUI (будет переписан на вебсервер).
• 28.10.2019 — Перевод на Python3 by botanegg.
• 16.10.2019 — Исправление функции загрузки данных с росреестра by botanegg.
• 11.09.2018 — Исправление ошибки формирование полигональной геометрии при экспорте в GEOJSON #8 by denny123.
• 12.03.2018 — Исправление функции завершения выполнения операций в консоли при нажатии на Ctrl+C.
• 05.03.2018 — Добавлена возможность загрузки через прокси #7 by Niakr1s.
• 09.03.2017 — Добавлена поддержка пользовательского интерфейса с интерактивной картой.
• 17.10.2016 — Увеличена точность вычисления контуров участков.
• 14.10.2016 — Обработка участков с несколькими полигонами.
• 06.10.2016 — Осуществление экспорта таблиц в формате csv.
• 05.10.2016 — Пакетная загрузка участков по списку кадастровых номеров из файла, перевод координат в WGS84.
• 03.10.2016 — Добавлена возможность выбора типа площади.
• 05.09.2016 — Изменен формат записи координат, добавлена возможность хранить мультиполигональную геометрию.
• 23.05.2016 — В тестовом режиме работает восстановление полигонов с отверстиями по PNG.
• 21.05.2016 — Были внесены изменения, чтобы вернуть работу с распознаванием точек по PNG. Упала точность, пропала способность рисовать полигоны и выделять отверстия.
• 21.05.2016 — На публичных кадастровых картах заблокировали SVG и внесли ещё некоторые изменения в работу сервисов. В связи с этим перестало работать приложение.