Как найти площадь неправильной фигуры

Какой способ лучше?

Второй и третий способы универсальные. Они помогут посчитать площадь даже самых замысловатых фигур. Вернемся еще раз ко второму способу.

Вот смотри, нужно посчитать площадь такой фигуры:

Окружаем ее прямоугольником и снова получаем одну нужную, но сложную площадь и много ненужных, но простых.

А теперь чтобы найти площадь \( \displaystyle S\) просто находим площадь прямоугольника и вычитаем из него оставшуюся площадь фигур на клетчатой бумаге \( \displaystyle {{S}_{1}}+{{S}_{2}}+{{S}_{3}}+{{S}_{4}}\).

\( \displaystyle {{S}_{прямоугольника}}=6\cdot 11=66\)\( \displaystyle {{S}_{1}}=\frac{1}{2}\cdot 6\cdot 4=12\)\( \displaystyle {{S}_{2}}=\frac{1}{2}\cdot a\cdot h=\frac{1}{2}\cdot 5\cdot 4=10\) (обрати внимание, \( \displaystyle {{S}_{2}}\) площадь НЕ прямоугольного треугольника, но все равно легко считается по основной формуле). \( \displaystyle {{S}_{3}}=\frac{1}{2}\cdot 5\cdot 2=5\)\( \displaystyle {{S}_{4}}=\frac{1}{2}\cdot 1\cdot 11=5,5\).Значит, \( \displaystyle S={{S}_{прямоугольника}}-{{S}_{1}}-{{S}_{2}}-{{S}_{3}}-{{S}_{4}}\)

\( \displaystyle {{S}_{3}}=\frac{1}{2}\cdot 5\cdot 2=5\)\( \displaystyle {{S}_{4}}=\frac{1}{2}\cdot 1\cdot 11=5,5\).Значит, \( \displaystyle S={{S}_{прямоугольника}}-{{S}_{1}}-{{S}_{2}}-{{S}_{3}}-{{S}_{4}}\).

\( \displaystyle S=66-12-10-5-5,5=33,5\)Вот и ответ: \( \displaystyle S=33,5\).Ну как тебе этот способ?

Вот смотри. С одной стороны, когда фигура занимает много клеточек, их замучаешься считать и можно ошибиться.

С другой стороны, когда мы дорисуем до прямоугольника, нужно считать много площадей.

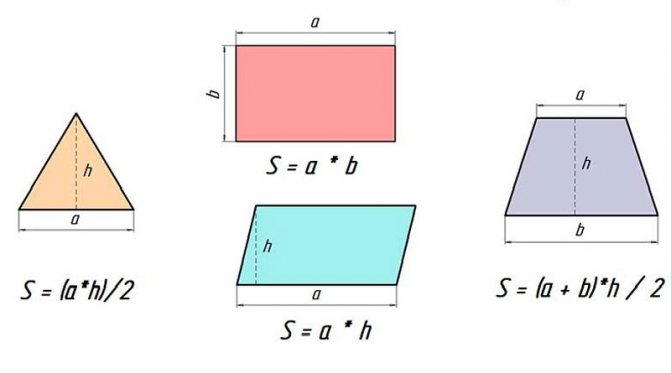
Формулы площади треугольника

1. Формула площади треугольника по стороне и высотеПлощадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты

   S =	1	a · h
   2

2. Как определить площадь четырехугольника

   Формула площади треугольника по трем сторонам

3. Формула площади треугольника по двум сторонам и углу между нимиПлощадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.

   S =	1	a · b · sin γ
   2

4. Формула площади треугольника по трем сторонам и радиусу описанной окружности

   S =	a · b · с
   4R

5. Формула площади треугольника по трем сторонам и радиусу вписанной окружностиПлощадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.

   S = p · r

   где S – площадь треугольника,a, b, c – длины сторон треугольника,h – высота треугольника,γ – угол между сторонами a и b,r – радиус вписанной окружности, R – радиус описанной окружности,

   p =	a + b + c	– полупериметр треугольника.
   2

Советы и рекомендации

• Учитывайте неровности стен. Вертикали и горизонтали в многоквартирных домах часто отклоняются от идеальных показателей. В этом случае лучше брать среднюю величину, а замеры производить рядом с плинтусами и в центральной части.
• Для отметки ровных осей будет полезен лазерный уровень.
• Если не удается определить периметр сложной конструкции, то вдоль плинтуса можно уложить веревку. Затем ее распрямляют и измеряют.
• Для измерения вертикалей используйте отвес: веревку с грузом закрепляют на самой высокой точке, затем ее можно снять и измерить. Отвес всегда показывает перпендикуляр к линии горизонта.

Источники

• https://DomaVlad.ru/sovety-dlya-doma/kak-poschitat-kvadratnye-metry.html
• https://stroim.guru/polezno-znat/kvadratnyj-metr-eto-skolko.html
• https://J.Etagi.com/ps/kak-uznat-ploshchad-komnaty/
• https://www.sdvor.com/articles/kak-poschitat-ploshchad-sten/

Объем комнаты

Кубатура помещения, или объём в строительстве используется при подсчёте необходимой мощности отопления, вентиляции, кондиционирования комнаты. Объём измеряется в кубических метрах. Единица записывается как 1 м³.

С точки зрения геометрии, помещение как фигура представляет собой шестигранник.

Измерив длину, ширину и высоту комнаты прямоугольной формы, перемножив полученные измерения, получают объём простого помещения.

Объём помещения сложной формы вычисляют следующим путём:

• пол комнаты разбивают на простые геометрические фигуры;
• вычисляют квадратуру каждой фигуры;
• полученные значения складывают и умножают на высоту до потолка.

Вычислить, найти площадь геометрических фигур

Онлайн Расчеты и формулы площади для плоских фигур
Площадь треугольника калькулятор нахождения площади треугольников	Площадь прямоугольного треугольника онлайн формула площади прямоугольного треугольника
Площадь равнобедренного треугольника найти площади равнобедренных треугольников	Площадь равностороннего треугольника вычислить площадь равностороннего треугольника
Площадь треугольника по формуле Герона площадь Герона, формула	Площадь квадрата чему равна площадь квадрата
Площадь прямоугольника как найти чему равна площадь прямоугольника	Площадь круга онлайн калькулятор площади круга через радиуса
Площадь ромба как найти площадь ромба через диагонали и т.д.	Площадь параллелограмма онлайн калькулятор для нахождения площади параллелограмма
Площадь трапеции площадь прямоугольной и равнобедренной трапеции	Площадь эллипса формула площади эллипса онлайн
Площадь кольца как вычислить площадь кольца онлайн	Площадь четырехугольника чему равна площадь четырехугольника, формула
Площадь сектора кольца подсчитать площади сектора кольца	Площадь сектора круга получить площадь сектора круга
Площадь сегмента круга решить площадь сегмента круга
Онлайн Расчеты и формулы площади для объемных фигур
Площадь шара калькулятор нахождения площадь поверхности сферы или шара	Площадь куба как найти чему равна площадь поверхности куба
Площадь цилиндра калькулятор для нахождения площади поверхности и основания цилиндра	Площадь пирамиды формулы расчета площади боковой поверхности и основания пирамиды
Площадь параллелепипеда калькулятор площади параллелепипеда прямоугольного и др.	Площадь конуса нахождение площади поверхностей конуса
Площадь усеченного конуса калькулятор нахождения площади поверхности усеченного конуса	Площадь тетраэдра площадь поверхности и грани тетраэдра
Площадь призмы калькулятор нахождения площади поверхности и боковой площади призмы

Площадь фигуры сложной формы может составляться из различных элементарных фигур: треугольников, квадратов, прямоугольников и пр. Общая площадь будет высчитываться путем суммирования площадей составляющих компонент.

Набор онлайн-калькуляторов страницы дает возможность оперативного вычисления не только S плоских фигур (квадрата, прямоугольника, круга, ромба, эллипса), но и площадей объемных фигур (куба, призмы, конуса, цилиндра, сферы, тетраэдра и пр.), являющихся совокупностью нескольких плоскостей.

Вычисление площадей фигур востребовано для решения различных задач: — строительных; — кадастровых; — инженерных и пр.

Государство осуществляет кадастровый учет земельных участков, основным учитываемым параметром которых является площадь. Специалистами БТИ фиксируется общая и полезная жилая площадь квартир. В быту иногда нужно вычислять площадь ковра, натяжного потолка, площадь дачного участка и пр.

Источник

Площадь комнаты

Знание метража комнаты пригодится для определения стоимости полового покрытия, отделки потолка, количества и мощности осветительных приборов. Замеряя квадратуру помещения, проверяют соответствие площади, заявленной по проекту.

Измерения стен удобнее производить снизу, на уровне плинтуса. Сомнения в правильной форме помещения устраняют при помощи измерения диагоналей. Если диагонали комнаты равны, то углы – прямые, а помещение – прямоугольное.

Квадрат или прямоугольник

Самая распространенная форма комнаты в плане – квадратная или прямоугольная. Подсчёт квадратуры по полу при этом не составит особого труда:

• измеряют с помощью рулетки длину и ширину комнаты;
• перемножают цифры между собой, записывая результат на бумагу;
• выступы, колонны обмеряют, площадь элементов считают по тем же принципам, перемножая два размера;
• получившиеся цифры вычитают из площади комнаты.

При этом площадь потолка считают по тому же принципу, то есть умножают длину на ширину за вычетом технологических проемов, если таковые имеются.

Посчитав квадратные метры помещений и сложив их, можно узнать площадь всего дома.

Помещение неправильной формы

Эркеры, мансарды и комнаты домов со сложной архитектурой в плане часто имеют неправильную форму. Метраж нестандартной комнаты с полукругами, выступами, множеством углов подсчитать сложнее. Облегчают задачу, используя принцип деления сложных фигур на простые.

Пол, представляя как составную фигуру мысленно или отображая на бумаге, разделяют на стандартные геометрические элементы. Затем вычисляют площадь элементов по одному и складывают полученные величины.

Г-образные, Т-образные формы помещения в плане разбивают на прямоугольники и квадраты. Полукруглые поверхности принимают как часть круга.

Количество квадратных метров пола комнаты, в основе которой лежит трапеция, можно высчитать двумя способами:

• представив трапецию, как сочетание квадрата с двумя треугольниками. Получив значение фигур, цифры складывают;
• по формуле площади трапеции.

Для подсчёта по формуле измеряют две противоположные длинные стены, эти размеры дадут значения оснований. Значение высоты определяют путём замера перпендикуляра, проведённого от одного из углов меньшего основания к большему.

Формула площади трапеции S=1/2(А+В)*Н, где:

• S – искомая величина, площадь трапеции;
• А – основание трапеции;
• В – основание трапеции;
• Н – высота трапеции.

Площадь трапециевидной комнаты – половина суммы числовых значений оснований, умноженных на высоту.

Формулы для площадей четырехугольников

Четырехугольник	Рисунок	Формула площади	Обозначения
		S = ab	a и b – смежные стороны
		d – диагональ,φ – любой из четырёх углов между
	S = 2R2 sin φ Получается из верхней формулы подстановкой d=2R	R – радиус ,φ – любой из четырёх углов между
		S = a ha	a – сторона,ha – , опущенная на эту сторону
	S = absin φ	a и b – смежные стороны,φ – угол между ними
		d1, d2 – , φ – любой из четырёх углов между ними
		S = a2	a – сторона квадрата
	S = 4r2	r – радиус
		d – квадрата
	S = 2R2 Получается из верхней формулы подстановкой d = 2R	R – радиус
		S = a ha	a – сторона,ha – , опущенная на эту сторону
	S = a2 sin φ	a – сторона,φ – любой из четырёх углов ромба
		d1, d2 –
	S = 2ar	a – сторона,r – радиус
		r – радиус ,φ – любой из четырёх углов ромба
			a и b – основания,h –
	S = m h	m – ,h –
		d1, d2 – , φ – любой из четырёх углов между ними
		a и b – основания,c и d  – боковые стороны
		S = ab sin φ	a и b – неравные стороны,φ – угол между ними
		a и b – неравные стороны,φ1 – угол между сторонами, равными a ,φ2 – угол между сторонами, равными b.
	S = (a + b) r	a и b – неравные стороны,r – радиус
		d1, d2 –
Произвольный выпуклый четырёхугольник			d1, d2 – , φ – любой из четырёх углов между ними
		,	a, b, c, d – длины сторон четырёхугольника,p – , Формулу называют «Формула Брахмагупты»

	S = ab гдеa и b – смежные стороны
	гдеd – диагональ,φ – любой из четырёх углов между
	S = 2R2 sin φ гдеR – радиус ,φ – любой из четырёх углов между Формула получается из верхней формулы подстановкой d = 2R
	S = a ha гдеa – сторона,ha – , опущенная на эту сторону
	S = absin φ гдеa и b – смежные стороны,φ – угол между ними
	гдеd1, d2 – , φ – любой из четырёх углов между ними
	S = a2 гдеa – сторона квадрата
	S = 4r2 гдеr – радиус
	гдеd – квадрата
	S = 2R2 гдеR – радиус Получается из верхней формулы подстановкой d = 2R
	S = a ha гдеa – сторона,ha – , опущенная на эту сторону
	S = a2 sin φ гдеa – сторона,φ – любой из четырёх углов ромба
	гдеd1, d2 –
	S = 2ar гдеa – сторона,r – радиус
	гдеr – радиус ,φ – любой из четырёх углов ромба
	гдеa и b – основания,h –
	S = m h гдеm – ,h –
	гдеd1, d2 – , φ – любой из четырёх углов между ними
	гдеa и b – основания,c и d  – боковые стороны
	S = ab sin φ гдеa и b – неравные стороны,φ – угол между ними
	гдеa и b – неравные стороны,φ1 – угол между сторонами, равными a ,φ2 – угол между сторонами, равными b.
	S = (a + b) r гдеa и b – неравные стороны,r – радиус
	гдеd1, d2 –
Произвольный выпуклый четырёхугольник
	гдеd1, d2 – , φ – любой из четырёх углов между ними
	, гдеa, b, c, d – длины сторон четырёхугольника,p – Формулу называют «Формула Брахмагупты»

S = ab гдеa и b – смежные стороны

гдеd – диагональ,φ – любой из четырёх углов между

S = 2R2 sin φ гдеR – радиус ,φ – любой из четырёх углов между Формула получается из верхней формулы подстановкой d = 2R

S = a ha гдеa – сторона,ha – , опущенная на эту сторону

S = absin φ гдеa и b – смежные стороны,φ – угол между ними

гдеd1, d2 – , φ – любой из четырёх углов между ними

S = a2 гдеa – сторона квадрата

S = 4r2 гдеr – радиус

гдеd – квадрата

S = 2R2 гдеR – радиус Получается из верхней формулы подстановкой d = 2R

S = a ha гдеa – сторона,ha – , опущенная на эту сторону

S = a2 sin φ гдеa – сторона,φ – любой из четырёх углов ромба

гдеd1, d2 –

S = 2ar гдеa – сторона,r – радиус

гдеr – радиус ,φ – любой из четырёх углов ромба

гдеa и b – основания,h –

S = m h гдеm – ,h –

гдеd1, d2 – , φ – любой из четырёх углов между ними

гдеa и b – основания,c и d  – боковые стороны,

S = ab sin φ гдеa и b – неравные стороны,φ – угол между ними

гдеa и b – неравные стороны,φ1 – угол между сторонами, равными a ,φ2 – угол между сторонами, равными b.

S = (a + b) r гдеa и b – неравные стороны,r – радиус

гдеd1, d2 –

Произвольный выпуклый четырёхугольник

гдеd1, d2 – , φ – любой из четырёх углов между ними

гдеa, b, c, d – длины сторон четырёхугольника,p – Формулу называют «Формула Брахмагупты»

Инструкция для калькулятора расчета площади земельного участка неправильной формы

Впишите размеры сторон AB, BC, CD, DA в метрах.

Замеры участка проводят, с помощью длинной рулетки, лазерного дальномера, мерного колеса. Также можно изготовить деревянную треногу (наподобие циркуля) зафиксировав расстоянием между «ногами» в 1 м и, шагая таким приспособлением вдоль границы делянки подсчитать количество шагов.

Нажмите «Рассчитать».

Онлайн калькулятор позволяет определить площадь (в квадратных метрах, сотках, акрах и гектарах) земельного участка или поля, имеющего неправильную форму. Это пригодится для корректного оформления документов права собственности на землю, продажи, сдачи в аренду или его деления (т.н. межевания) без применения топографической съемки и специальных картографических программ. Также иногда просто нужно посчитать сколько соток имеет участок, чтобы прикинуть его рыночную стоимость.

Источник

Советы и рекомендации

• Учитывайте неровности стен. Вертикали и горизонтали в многоквартирных домах часто отклоняются от идеальных показателей. В этом случае лучше брать среднюю величину, а замеры производить рядом с плинтусами и в центральной части.
• Для отметки ровных осей будет полезен лазерный уровень.
• Если не удается определить периметр сложной конструкции, то вдоль плинтуса можно уложить веревку. Затем ее распрямляют и измеряют.
• Для измерения вертикалей используйте отвес: веревку с грузом закрепляют на самой высокой точке, затем ее можно снять и измерить. Отвес всегда показывает перпендикуляр к линии горизонта.

Источники

• https://DomaVlad.ru/sovety-dlya-doma/kak-poschitat-kvadratnye-metry.html
• https://stroim.guru/polezno-znat/kvadratnyj-metr-eto-skolko.html
• https://J.Etagi.com/ps/kak-uznat-ploshchad-komnaty/
• https://www.sdvor.com/articles/kak-poschitat-ploshchad-sten/

Обозначение площади

Площадь — это одна из характеристик замкнутой геометрической фигуры, которая дает нам информацию о ее размере. S (square) — знак площади.

Если параметры фигуры переданы в разных единицах длины, мы не сможем решить ни одну задачу. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.

Популярные единицы измерения

• квадратный миллиметр (мм 2 );
• квадратный сантиметр (см 2 );
• квадратный дециметр (дм 2 );
• квадратный метр (м 2 );
• квадратный километр (км 2 );
• гектар (га).

Круг — это когда множество точек на плоскости удалены от центра на равном радиусу расстоянии. Радиусом принято называть прямую линию, соединяющую центр с любой точкой окружности.

1. S = π * r 2 , где r — это радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.

2. S = d 2 : 4 * π, где d — это диаметр.

3. S = L 2 ​ : 4 * π, где L — это длина окружности.

Примеры решения

Задачи на нахождение площади применяются в нескольких дисциплинах. В геометрии применяются различные комбинации, при которых известны некоторые величины:

1. Две стороны.
2. Одна из сторон и диагональ.
3. Диагональ и разность сторон.

Для расчета расходных материалов и площади поперечного сечения проводника можно всегда измерить стороны прямоугольника. Существует два способа нахождения: автоматизированный и ручной. В первом случае используется специализированное программное обеспечение. Однако вовсе не обязательно применять сложные алгоритмы и программные модули, поскольку формула является очень простой. Для расчета специалисты рекомендуют применять онлайн-калькулятор.

При ручном режиме расчета нужно подставлять значения в формулу. После этого выполнять вычисления. Возможна и оптимизация процесса вычисления. Для этой цели рекомендуется использовать Excel. Приложение входит в состав стандартного офисного пакета MS Office.

Геометрия на плоскости

Задача сводится к тому, что необходимо высчитать S, зная размеры сторон (a = 25 и b = 10). В этом случае следует воспользоваться базовой формулой: S = a * b = 25 * 10 = 250 (ед 2 ). В ответе указывается условная единица измерения, поскольку явная не указана в условии задачи.

Еще один вариант задания немного сложнее предыдущего. Он имеет следующее условие: одна из сторон прямоугольника равна 6 м и диагональ 10 м. Нужно найти площадь прямоугольника. Формулой в этом случае является теорема Пифагора. Треугольник, который образуется при проведении диагонали, считается прямоугольный (неравносторонний, а разносторонний). Решается задача следующим образом:

Находится неизвестная сторона: b =(d 2 — a 2 )^(1/2) = (100 — 36)^(1/2) = 8 (м).

Площадь (произведение сторон): S = 6 * 8 = 48 (м 2 ).

Можно использовать двойную формулу Герона, однако метод усложняет вычисления. Для сравнения скорости и объема вычислений следует решить задачу вторым способом:

Значение площади будет вычисляться таким образом: S = 2 * ^(1/2) = 2 * 24 = 48 (м 2 ).

Второй способ считается неправильным, поскольку необходимо во всех задачах оптимизировать вычисления. Сложным типом задачи, кроме интегрирования, считается нахождение площади, когда неизвестны стороны, а известна только диагональ (10). Известно также, что одна из сторон больше другой на 3 метра. В этом случае надо выражать одну сторону через другую. Алгоритм решения следующий:

1. Обозначить стороны: a = x и b = x — 3.
2. Составить уравнение: x * (x — 3) = 10.

Раскрыть скобки: x 2 — 3x — 10 = 0.

Нахождение дискриминанта: D = b 2 — 4* a * c = 9 — (4 * 10) 2 ). Однако берется не исходное значение, а приближенное. Его нужно округлять только в большую сторону, т. е. править 3,75 на значение 4. Следует руководствоваться таким правилом: результат округляется в большую сторону.

Источник

Площадь комнаты в квадратных метрах

Посчитать несложно, требуется только вспомнить простейшие формулы а также провести измерения. Для этого нужны будут:

• Рулетка. Лучше — с фиксатором, но подойдет и обычная.
• Бумага и карандаш или ручка.
• Калькулятор (или считайте в столбик или в уме).

Набор инструментов нехитрый, найдется в каждом хозяйстве. Проще измерения проводить с помощником, но можно справиться и самостоятельно.

Для начала надо измерить длину стен. Делать это желательно вдоль стен, но если все они заставлены тяжелой мебелью, можно проводить измерения и посередине. Только в этом случае следите чтобы лента рулетки лежала вдоль стен, а не наискосок — погрешность измерений будет меньше.

Прямоугольная комната

Если помещение правильной формы, без выступающих частей, вычислить площадь комнаты просто. Измеряете длину и ширину, записываете на бумажке. Цифры пишите в метрах, после запятой ставите сантиметры. Например, длина 4,35 м (430 см), ширина 3,25 м (325 см).

Как высчитать площадь комнаты

Найденные цифры перемножаем, получаем площадь комнаты в квадратных метрах. Если обратимся к нашему примеру, то получится следующее: 4,35 м * 3,25 м = 14,1375 кв. м. В данной величине оставляют обычно две цифры после запятой, значит округляем. Итого, рассчитанная квадратура комнаты 14,14 квадратных метров.

Помещение неправильной формы

Если надо высчитать площадь комнаты неправильной формы, ее разбивают на простые фигуры — квадраты, прямоугольники, треугольники. Потом измеряют все нужные размеры, производят расчеты по известным формулам (есть в таблице чуть ниже).

Перед тем как посчитать площадь комнаты, тоже проводим изменения. Только в этом случае цифр будет не две, а четыре: добавится еще длина и ширина выступа. Габариты обоих кусков считаются отдельно.

Один из примеров — на фото. Так как и то, и другое — прямоугольник, площадь считается по той же формуле: длину умножаем на ширину. Найденную цифру надо отнять или прибавить к размеру помещения — в зависимости от конфигурации.

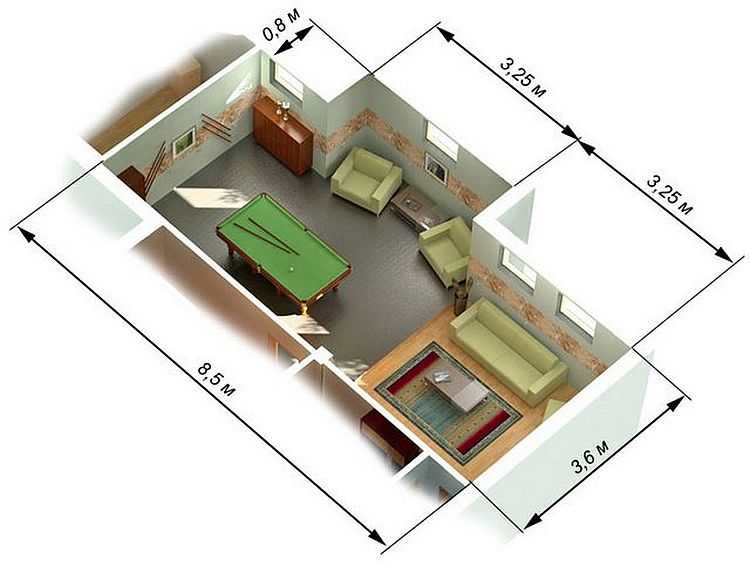
Площадь комнаты сложной формы

Покажем на этом примере как посчитать площадь комнаты с выступом (изображена на фото выше):

1. Считаем квадратуру без выступа: 3,6 м * 8,5 м = 30,6 кв. м.
2. Считаем габариты выступающей части: 3,25 м * 0,8 м = 2,6 кв. м.
3. Складываем две величины: 30,6 кв. м. + 2,6 кв. м. = 33,2 кв. м.

Еще бывают помещения со скошенными стенами. В этом случае разбиваем ее так, чтобы получились прямоугольники и треугольник (как на рисунке ниже). Как видите, для данного случая требуется иметь пять размеров. Разбить можно было по-другому, поставив вертикальную, а не горизонтальную черту

Это не важно. Просто требуется набор простых фигур, а способ их выделения произвольный

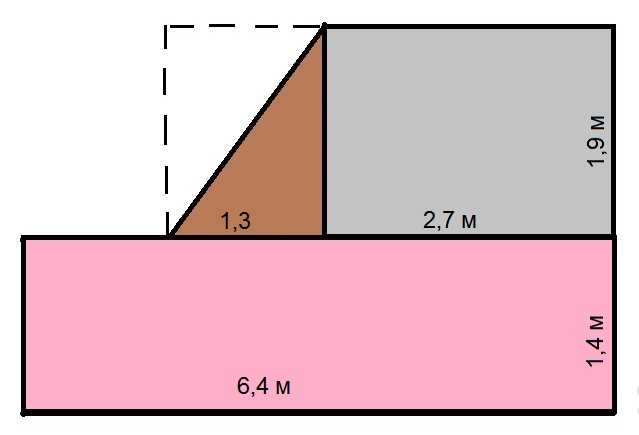
Как посчитать площадь комнаты неправильной формы

В этом случае порядок вычислений такой:

1. Считаем большую прямоугольную часть: 6,4 м * 1,4 м = 8,96 кв. м. Если округлить, получим 9, 0 кв.м.
2. Высчитываем малый прямоугольник: 2,7 м * 1,9 м = 5,13 кв. м. Округляем, получаем 5,1 кв. м.
3. Считаем площадь треугольника. Так как он с прямым углом, то равен половине площади прямоугольника с такими же размерами. (1,3 м * 1,9 м) / 2 = 1,235 кв. м. После округления получаем 1,2 кв. м.
4. Теперь все складываем чтобы найти общую площадь комнаты: 9,0 + 5,1 + 1,2 = 15,3 кв. м.

Планировка помещений может быть очень разнообразной, но общий принцип вы поняли: делим на простые фигуры, измеряем все требуемые размеры, высчитываем квадратуру каждого фрагмента, потом все складываем.

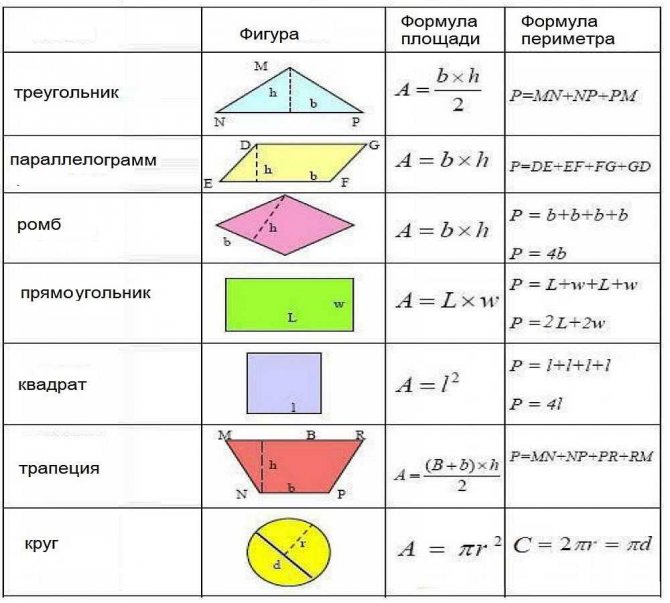
Формулы расчета площади и периметра простых геометрических фигур

Еще одно важное замечание: площадь комнаты, пола и потолка — это все одинаковые величины. Отличия могут быть если есть какие-то полу-колоны, не доходящие до потолка

Тогда из общей квадратуры вычитается квадратура этих элементов. В результате получаем площадь пола.

Измеряем площадь сложных фигур

Круг и треугольник – сложные фигуры для самостоятельного вычисления

. Как измерить квадратные метры окружности, если нет математического или инженерного образования? Опять-таки по формуле.

Как измерить размер окружности

Существует формула вычисления площади круга. Есть такое постоянное число – отношение длины окружности к ее диаметру. Оно одинаково для всех размеров круга. Называется оно пи и равняется 3,14. Вот это число и используют при подсчетах.

• Этап № 1. Замеряем диаметр (это линия, которая проходит через центр круга от одного края окружности к другому). Пускай диаметр будет равняться 3 м. Далее находим радиус – это половина длины диаметра. То есть 1,5 м. Записываем радиус на бумагу.
• Этап № 2. Производим расчеты по формуле S = ПR2, где S – это площадь круга, П – постоянное число, а R – радиус окружности. Получается 3,14 x (1,5 x 1,5) = 7, 065. Площадь данного круга – 7,065 кв. м.

Методика выполнения работы

Перед тем, как рассчитать квадратуру дома, нужно подготовить следующее:

1. Калькулятор для проведения вычислений. 
2. Рулетка для проведения измерений. При этом надо учитывать, что некоторые производят измерения в дюймах – они не подойдут. Нужна рулетка, которая указывает длину с помощью сантиметров. 
3. Потребуется план квартиры. Измерение площади стен, пола и потолка будет выполняться на его основе. Если такую схему найти нельзя, то её нужно нарисовать от руки, стремясь реалистично отобразить размеры и геометрическую форму частей. 
4. Также потребуется бумага и карандаш для ведения записей в процессе работы. 

При замерах полов, стен и потолков в первую очередь потребуются знания из школьной геометрии. Простейшим способом, как рассчитать площадь дома в квадратных метрах, является вычисление прямоугольных поверхностей. Площадь прямоугольника вычисляется как произведение его сторон. 

Вычисление площади простейших геометрических фигур основано на базовых формулах из геометрииИсточник stroychik.ru

При этом важно учитывать следующее.

Хотя на вид комната состоит из прямоугольных деталей, на самом деле это может оказаться немного по-другому. Например, ширина стен, измеренная с одной и другой стороны, может отличаться на несколько сантиметров. Эта проблема особенно существенна при измерении расстояний в домах старой постройки. В таких случаях обычно измеряют длину в нескольких местах, а при вычислении площади используют среднее значение. 
Вычисления позволяют получить нужные цифры с высокой точностью

Однако будет разумной предосторожностью при вычислениях добавить к площади небольшую величину. Это позволит исключить ситуацию, в которой стройматериалов чуть-чуть не хватило. 

Таким способом можно вычислить площадь прямоугольных пустых стен, пола и потолка.
 

Сложная форма стен и потолка может быть разделена на простые фигуры для упрощения вычисленийИсточник www.buvbaze.lv

Расчёт площади стен с окнами и дверьми

Если на стене есть окно или дверь, то вычисление производится следующим образом:

• Определяется площадь стены без учёта двери или окна. 
• Вычисляется площадь каждого окна или двери путём умножения их длины на ширину. 
• Из площади стены вычитают площадь окон и дверей. 

Этот способ применим в тех случаях, когда рассматриваются прямоугольные стены.

Площадь стены, имеющей неправильную форму

В этом случае нужно разделить вычисления на этапы. Стена с нишами может иметь сложную форму. Однако её всегда можно условно разбить на несколько участков, каждый из которых соответствует одной из простых форм. Затем надо рассчитать площади каждой из частей и сложить их. 

Как посчитать площадь стен, рассказано в видео

Расчёт через периметр

Если комната имеет неправильную форму, то площадь стен можно вычислить, измерив длину периметра. В этом случае проводят измерение горизонтальных отрезков по каждой из сторон помещения и складывают их вместе, затем определяют высоту. Произведение этих величин равно площади стен в этом помещении. 

Несколько советов

• Нужно при проведении расчётов все цифры наносить на план. Таким образом сохранится не только результат, но и промежуточные вычисления, которые могут пригодится при проведении ремонтных работ в будущем. 
• При вычислении площади нужно учитывать, что не всегда необходима полная величина. Например, обои могут клеить не только на всю стену, а на их часть. Класть плитку могут до потолка либо только до определённой высоты. Поэтому нужно точно определить, как высчитать квадратуру дома с учётом конкретного плана ремонта. 

Как сделать замеры – можно посмотреть в видеоролике:

Для того, чтобы точно знать, сколько необходимо стройматериалов для проведения работ, нужно учитывать площади стен, пола и потолка, а также нормы расхода стройматериалов. Среднюю величину расхода можно узнать, спросив у продавцов, а квадратуру дома необходимо измерить самостоятельно. Для этого нужно воспользоваться знаниями из элементарной геометрии. При вычислении площади сложных фигурных поверхностей их разбивают на простые части, делают необходимые вычисления, затем суммируют их. 

Определение площади сложной фигуры с помощью теории вероятностей

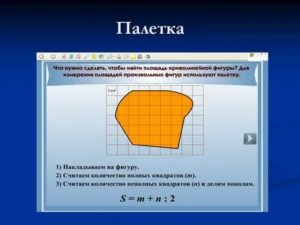
Да мало ли зачем. Например, возникла необходимость определить площадь территории на карте.

Конечно, можно посмотреть в справочнике или поискать в интернете, но иногда и территории бывают нестандартными — допустим, вы озаботились проблемами лесов в пойме Амазонки и хотите ежемесячно измерять площадь зелёных пятен на фотографиях со спутника.

Если вы ботаник (в хорошем смысле слова), то вам может понадобиться измерить площадь листовой поверхности разных сортов одного растения. Или, к примеру, более прозаичная задача — нужно зашпатлевать кусок стены, а банки шпатлёвки хватает только на 1 кв. м. — нужно выяснить, покупать одну банку или раскошелиться на две.

В чём сложность нахождения площади?

Конечно, если фигура представляет собой прямоугольник, круг или, что хуже, эллипс, то проблема решается с помощью Google и калькулятора. Но где бы найти формулу, да попроще, для нахождения площади, скажем, такого рисунка?

Теория вероятностей, Ваш выход!

Сразу оговорюсь, что теория вероятностей по своей сути не подразумевает точного решения задач. Так будет и в этом случае — если вам нужна космическая точность, то предлагаю копать в сторону методов имитационного моделирования. Если же погрешность в пределах 2-5% вас вполне устраивает, то будет достаточно того же калькулятора, базовых навыков программирования и умения считать до ста.

Суть метода

Суть метода проста до банальности. Допустим, мы пасмурным деньком выложили капустный листочек (см. ремарку про биолога выше) на прямоугольный поддон, а поддон выставили под накрапывающий дождик.

А потом засекли определённое время (к примеру, пять минут) и посчитали, сколько капелек упало на поддон, а сколько непосредственно на лист.

Если принять во внимание, что дождь обычно капает равномерно, то получается простая пропорция — лист во столько раз меньше поддона, во сколько раз на него упало меньше капель дождя, чем на весь поддон

Возвращаемся к нашей фигуре

Итак, как же определить площадь той розовой пятерни? Да очень просто — заключить фигуру в прямоугольные границы и проставить случайным образом много точек. Чем больше, тем лучше (в соответствии с законом больших чисел). А потом подсчитать количество точек, попавших на фигуру.

Я намеренно не обсуждаю вопросы реализации такого алгоритма, потому что вариантов масса. Можно просто закрыть глаза и наугад тыкать шариковой ручкой, а можно действовать более научно — с помощью языков программирования.

Например, код на PHP занял у меня не больше 15 строчек, а в результате получилось вот что: Точки общим числом 300, разумеется, проставлены с помощью генератора случайных чисел.

Для удобства подсчета точек я разбил изображение на 36 секторов — теперь нужно подсчитать количество точек, попавших на изображение, в каждом секторе, а результаты сложить.

Сведём данные в таблицу (ячейка таблицы соответствует сектору на картинке):

4	8	4
7	5	6	4
3	6	13	7	8	5
1	10	10	13	7	2
2	3	7	10	2
2	5	3

Теперь у нас есть все данные для того, чтобы вычислить площадь розовой пятерни: площадь описанного прямоугольника — 20 см х 20 см = 400 кв. см; количество точек в прямоугольнике — 300; количество точек внутри фигуры (сумма значений из таблицы) — 157;

площадь фигуры – 209,33 кв. см.

И насколько это точно?

Действительно, осталось определиться с точностью данного метода. Конечно, всё зависит от количества точек, и здесь нужно соблюдать золотую середину — десяти для нашего примера было бы явно недостаточно, а от тысячи слишком рябило бы в глазах. Поэтому попробуем определить погрешность для трёхсот точек и описанного квадрата со стороной 20 см.

Для этого возьмём фигуру, площадь которой нам известна заранее.

Например, такую: Проставляем точки: Результаты заносим в таблицу:

6	11	8	5
9	15	8	5	13	2
11	8	5	14	13	5
10	11	8	8	4	4
2	14	9	10	4	1
3	5	6

Рассчитываем площадь фигуры: площадь описанного прямоугольника — 20 см х 20 см = 400 кв. см; количество точек в прямоугольнике — 300; количество точек внутри фигуры (сумма значений из таблицы) — 237;

площадь фигуры – 316 кв. см.

Нетрудно посчитать, что реальная площадь круга с радиусом 10 см составляет 314,16 кв. см. Таким образом, погрешность метода составила 0,59%, чего в большинстве случаев достаточно для прикладного использования.

• теория вероятностей
• площадь фигуры

Хабы:

Вывод формул для площадей четырехугольников

      Утверждение 1. Площадь выпуклого четырёхугольника можно найти по формуле

где  d₁ и d₂ – , а φ – любой из четырёх углов между ними (рис. 1).

Рис. 1

      Доказательство. В соответствии с рисунком 1 справедливо равенство:

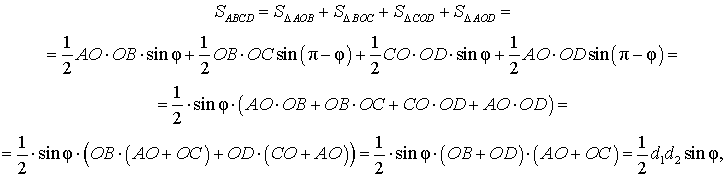
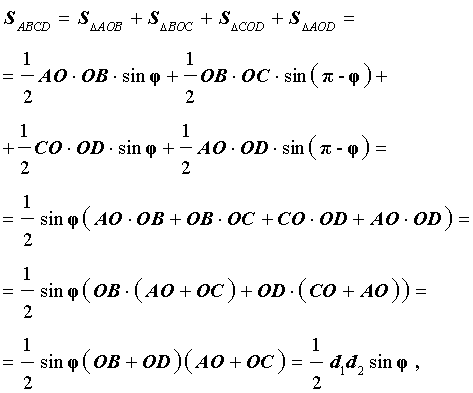
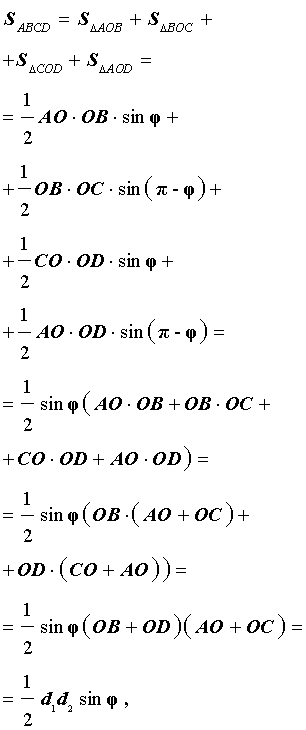
что и требовалось доказать.

      Утверждение 2. Площадь можно найти по формуле

S = a h_a ,

где a – сторона параллелограмма, а h_a – , опущенная на эту сторону (рис. 2).

Рис. 2

      Доказательство. Поскольку (рис.26), то четырёхугольник AEFB – прямоугольник. Поэтому

S_ABCD = S_AEFD = a h_a ,

что и требовалось доказать.

      Утверждение 3.Площадь можно найти по формуле

S = ab sin φ,

где a и b – смежные стороны параллелограмма, а φ – угол между ними (рис. 3).

Рис. 3

      Доказательство. Поскольку

h_a = b sin φ,

то, в силу утверждения 2, справедлива формула

S = a h_a = ab sin φ,

что и требовалось доказать.

      Утверждение 4. Площадь можно найти по формуле

,

где r – радиус , а φ – любой из четырёх углов ромба (рис.4).

Рис. 4

      Доказательство. Поскольку каждая из ромба является биссектрисой угла, а . Отсюда следует, в частности, что высота ромба в 2 раза больше радиуса вписанной окружности (рис.4). Поэтому

что и требовалось доказать.

      Утверждение 5. Площадь можно найти по формуле

,

где a и b – основания трапеции, а h  –  (рис.5).

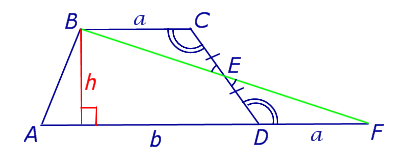
Рис. 5

      Доказательство. Проведём прямую BE через вершину B трапеции и середину E боковой стороны CD. Точку пересечения прямых AD и BE обозначим буквой F (рис. 5). Поскольку , то площадь трапеции ABCD равна площади треугольника ABF. Поэтому

что и требовалось доказать.

      Утверждение 6. Площадь можно найти по формуле

,

где a и b – основания, а c и d – боковые стороны трапеции, (рис.6).

Рис. 6

      Доказательство. Воспользовавшись , составим следующую систему уравнений с неизвестными x, y, h (рис. 6):

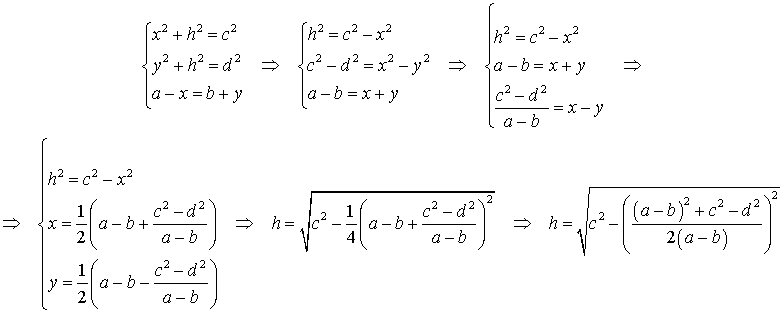
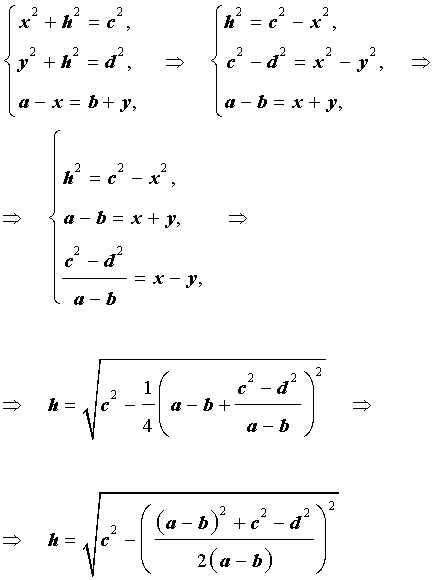
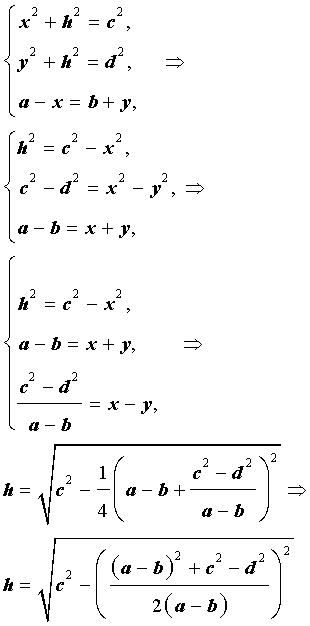
      Следовательно,

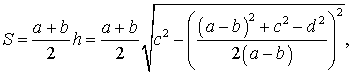
где

,

что и требовалось доказать.

      Утверждение 7. Площадь , , можно найти по формуле:

S = (a + b) r,

где a и b – неравные стороны дельтоида, а r – радиус (рис.7).

Рис. 7

      Доказательство. Докажем сначала, что в каждый дельтоид можно вписать окружность. Для этого заметим, что треугольники ABD и BCD равны в силу (рис. 7). Отсюда вытекает, что диагональ BD является биссектрисой углов B и D, а биссектрисы углов A и C пересекаются в некоторой точке O, лежащей на диагонали BD. Точка O и является центром вписанной в дельтоид окружности.

      Если r – радиус вписанной в дельтоид окружности, то

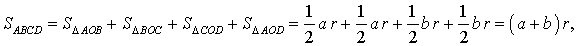
что и требовалось доказать.