Площадь пятиугольника онлайн калькулятор по сторонам

Содержание:

Для расчета площадь пятиугольника для начала нам нужно определить, регулярно это или нет. Пятиугольник — это многоугольник, замкнутая плоская фигура с пятью сторонами. Когда многоугольник правильный, это означает, что длина его сторон одинакова, а его внутренние углы одинаковы.

В этом случае есть формула для вычисления точной площади правильного многоугольника, зная некоторые из его основных характеристик, которые мы выведем позже.

Если многоугольник не правильный, то есть имеет стороны разных размеров и неравные внутренние углы, единой формулы не существует.

Однако математики нашли методы вычислений, такие как разделение фигуры на другие с меньшим количеством сторон, такие как треугольники, квадраты и прямоугольники, размеры которых легко узнать или вычислить.

Еще одна процедура для вычисления площадей полигонов в целом, зная координаты их вершин, — это метод, называемый Гауссовские детерминанты, о котором мы расскажем позже.

Площадь через квадрат[править | править код]

Площадь правильного восьмиугольника можно вычислить как площадь усечённого квадрата.

Площадь можно также вычислить как усечение квадрата

S=A2−a2,{\displaystyle S=A^{2}-a^{2},}

где A — ширина восьмиугольника (вторая меньшая диагональ), а a — длина его стороны. Это легко показать, если провести через противоположные стороны прямые, что даст квадрат. Легко показать, что угловые треугольники равнобедренные с основанием, равным a. Если их сложить (как на рисунке), получится квадрат со стороной a.

Если задана сторона a, то длина A равна

A=a2+a+a2=(1+2)a≈2.414213562373095a.{\displaystyle A={\frac {a}{\sqrt {2}}}+a+{\frac {a}{\sqrt {2}}}=(1+{\sqrt {2}})a\approx 2.414213562373095a.}

Тогда площадь равна:

S=((1+2)a)2−a2=2(1+2)a2≈4.82842712474619a2.{\displaystyle S=((1+{\sqrt {2}})a)^{2}-a^{2}=2(1+{\sqrt {2}})a^{2}\approx 4.82842712474619a^{2}.}

Площадь через A (ширину восьмиугольника)

S=2(2−1)A2≈0.8284271247461903A2.{\displaystyle S=2({\sqrt {2}}-1)A^{2}\approx 0.8284271247461903A^{2}.}

Ещё одна простая формула площади:

 S=2aA.{\displaystyle \ S=2aA.}

Часто значение A известно, в то время как величину стороны a следует найти, как, например, при отрезании от квадратного куска материала углов с целью получения правильного восьмиугольника. Из формул выше имеем

a≈A2.414213562373095.{\displaystyle a\approx A/2.414213562373095.}

Два катета углового треугольника можно получить по формуле

e=(A−a)2.{\displaystyle e=(A-a)/2.}

Физические формулы

142

Категории

6340

Формулы

2956

Переменные

Основные категориивсе категорииВсе формулы

физика
Аэродинамика
Невязкий, сжимаемый поток1 Больше!

Невязкий, несжимаемый поток4 Больше!

Вязкий поток

Текущее электричествоПотенциометр
Теория машин

Эластичность

ЭлектростатикаКонденсатор
Электромагнитная индукция
Электростатика
Магнитное поле из-за тока

Инженерная механикаКриволинейное движение

Динамика1 Больше!

Трение1 Больше!

Законы движения1 Больше!

Подъемные машины2 Больше!

Линейное движение2 Больше!

Движение связанных тел7 Больше!

Снаряды

Свойства поверхностей и твердых тел2 Больше!

Статика частиц

Устойчивость и управляемость полета
Характеристики самолета17 Больше!

Вступление2 Больше!

Статическая устойчивость и контроль13 Больше!

Механика жидкостиОсновы турбомашин
Течение пограничного слоя
Плавучесть
Центробежные насосы
Сжимаемый поток
Динамика потока жидкости
Поток в открытых каналах
Поток по трубам

Свойства жидкости3 Больше!

Гидравлические системы
Силы, развиваемые движущейся жидкостью
Силы на слитых телах
Фрэнсис Турбин
Гидравлические прямоходные приводы
Гидравлические моторы

Гидравлические насосы3 Больше!

Идеальный поток или потенциальный поток
Кинематика потока
Вырезы и водосливы
Отверстия и мундштуки
Пелтон Турбина
Поршневые насосы
Турбулентный поток
Вязкий поток

Газовая динамикаБазовый сжимаемый поток
Основы
Течение с трением и теплопередачей
Нормальные ударные волны
Косой удар и волны расширения

Газовые турбиныОсновы газовых турбин

Основы вращающихся машин1 Больше!

Газовые циклы3 Больше!

Впускные отверстия и сопла
Ракетная силовая установка

ГравитацияГравитационное поле
Гравитационный потенциал
Изменение ускорения под действием силы тяжести

ТепломассообменОсновы

Проведение4 Больше!

Конвекция3 Больше!

Конвективный массообмен

Внешний поток5 Больше!

Теплообменник3 Больше!

Увлажнение

Внутренний поток5 Больше!

Молярная диффузия

Радиация4 Больше!

Дизайн машины
Проектирование элементов машин98 Больше!

Материаловедение и металлургия
Кристаллография4 Больше!

Механические колебанияЭлементы вибрации
Принудительная вибрация
Свободная демпфированная вибрация

Свободная вибрация систем с одной степенью свободы1 Больше!

Система с несколькими степенями свободы
Система двух степеней свободы
Незатухающая свободная вибрация

Обработка металловЧип контроль
Смазочно-охлаждающая жидкость и шероховатость поверхности

Дизайн для обработки4 Больше!

ECM (электрохимическая обработка)3 Больше!

Экономика металлообрабатывающего производства9 Больше!

Шлифование2 Больше!

Станки и станки1 Больше!

Производственные системы и автоматизация

Механика резки металла1 Больше!

Номенклатура режущего инструмента
Нетрадиционные процессы обработки
Температуры резки металла

Срок службы и износ инструмента2 Больше!

Микроскопы и телескопыАстрономический телескоп
Составные микроскопы
Галилеев телескоп
Простой микроскоп
Земной телескоп

Современная физикаАтом
Ядро
Фотоэлектрический эффект
Вакуумные трубки и полупроводники

Оптика
давление

Технология производстваГеометрия токарного процесса
Merchant Force Circle (Механика ортогональной резки металла)
Резка металла и инструменты

Холодильное оборудование и кондиционирование воздуха
Системы кондиционирования воздуха1 Больше!

Циклы воздушного охлаждения1 Больше!

Системы воздушного охлаждения3 Больше!

Основы

Простые парокомпрессионные холодильные системы5 Больше!

Сопротивление материалов
Напряжение сдвига в балке7 Больше!

Напряжение изгиба в балке7 Больше!

Колонна и распорки17 Больше!

Прямое и изгибающее напряжение6 Больше!

Заклепочное соединение11 Больше!

Вращающийся диск и цилиндр8 Больше!

Стресс и напряжение19 Больше!

Толстые цилиндры и сферы5 Больше!

Тонкие цилиндры и сферы17 Больше!

Кручение валов и пружин18 Больше!

Сварные соединения8 Больше!

Теория машиныБалансировка вращающихся масс

Ременные, канатные и цепные приводы2 Больше!

Тормоза и динамометры6 Больше!

Кулачки2 Больше!

Трение

Фрикционные устройства1 Больше!

Поезда передач

Губернаторы5 Больше!

Кинематика движения2 Больше!

Кинетика движения

Механизм1 Больше!

Вращательное движение
Простые гармонические колебания
Клапаны и реверсивные механизмы паровых двигателей

Зубчатая передача3 Больше!

Диаграммы крутящего момента и маховик

Вибрации27 Больше!

Волновая оптикаИнтерференция волн двух интенсивностей
Разница оптического пути
Тонкопленочная интерференция
Эксперимент Юнга с двумя щелями

Волны и звук

Гауссовские детерминанты

Другой способ найти площадь неправильного пятиугольника или другого неправильного многоугольника — это поместить фигуру в декартову систему координат, чтобы найти координаты вершин.

Зная эти координаты, применяется гауссовский метод определителей для вычисления площади, которая определяется следующей формулой:

Где A — площадь многоугольника, а (x_п , Y_п ) — координаты вершин. Многоугольник с n сторонами имеет 5 вершин, для пятиугольника это будет n = 5:

Полосы, сопровождающие формулу, представляют собой столбцы модуля или абсолютного значения.

Это означает, что даже если результат операции отрицательный, мы должны выразить его положительным знаком, а если он уже положительный, то его нужно оставить с этим знаком. Это потому, что площадь всегда является положительной величиной.

Процедура названа гауссовскими детерминантами в честь ее создателя, немецкого математика Карла Ф. Гаусса (1777-1855). Указанные операции эквивалентны определителю матрицы 2 × 2, например, первый определитель равен:

Чтобы найти площадь пятиугольника, мы должны решить 5 определителей, сложить результат алгебраически, разделить его на 2 и, наконец, выразить площадь всегда с положительным знаком.

Симметрия[править | править код]

11 симметрий правильного восьмиугольника. Линии зеркальных отражений показаны цветом — синие линии проходят через вершины, фиолетовые проходят через середины рёбер, число поворотов указано в центре. Вершины раскрашены согласно симметрии.

Правильный восьмиугольник имеет группу симметрии Dih₈ порядка 16. Имеется 3 диэдральные подгруппы — Dih₄, Dih₂ и Dih₁, а также 4 циклические подгруппы — Z₈, Z₄, Z₂ и Z₁. Последняя подгруппа подразумевает отсутствие симметрии.

Правильный восьмиугольник имеет 11 различных симметрий. Джон Конвей обозначил полную симметрию как r16 . Диэдральные симметрии делятся на симметрии, проходящие через вершины (обозначены как d — от diagonal), или через рёбра (обозначены как p — от perpendiculars). Циклические симметрии в среднем столбце обозначены буквой g и для них указан порядок группы вращения. Полная симметрия правильного восьмиугольника обозначена как r16 а отсутствие — как a1.

Примеры восьмиугольников по их симметриям

r16
d8	g8	p8
d4	g4	p4
d2	g2	p2
a1

На рисунке слева показаны типы симметрий восьмиугольников. Наиболее общие симметрии восьмиугольников — p8, равноугольный восьмиугольник, построенный четырьмя зеркалами и имеющий перемежающиеся длинные короткие стороны, и d8, изотоксальный восьмиугольник, имеющий рёбра равной длины, но вершины имеют два разных внутренних угла. Эти две формы являются двойственным друг другу и имеют порядок, равный половине симметрии правильного восьмиугольника.

Каждая подгруппа симметрии даёт одну или более степеней свободы для неправильных форм. Только подгруппа g8 не имеет степеней свободы, но может рассматриваться как имеющая ориентированные рёбра.

Пример задачи

Условие. Координаты вершин заданы такими значениями (0.6; 2.1), (1.8; 3.6), (2.2; 2.3), (3.6; 2.4), (3.1; 0.5). Требуется вычислить площадь многоугольника.

Решение. По формуле, указанной выше, первое слагаемое будет равно (1.8 + 0.6)/2 * (3.6 — 2.1). Здесь нужно просто взять значения для игрека и икса от второй и первой точек. Несложный расчет приведет к результату 1.8.

Второе слагаемое аналогично получается: (2.2 + 1.8)/2 * (2.3 — 3.6) = -2.6. При решении подобных задач не стоит пугаться отрицательных величин. Все идет так, как нужно. Это планомерно.

Подобным образом получаются значения для третьего (0.29), четвертого (-6.365) и пятого слагаемых (2.96). Тогда итоговая площадь равна: 1.8 + (-2.6) + 0.29 + (-6.365) + 2.96 = — 3.915.

Применение восьмиугольников[править | править код]

Дорожный знак «Движение без остановки запрещено»

Восьмиугольный план Купола Скалы

В странах, принявших Венскую конвенцию о дорожных знаках и сигналах (в том числе в России), а также во многих других странах, знак «Движение без остановки запрещено» имеет вид красного восьмиугольника.

Восьмиугольные формы часто используются в архитектуре. Купол Скалы имеет восьмиугольный план. Башня Ветров в Афинах — ещё один пример восьмиугольной структуры. Восьмиугольный план встречается также в архитектуре церквей, таких как Собор Святого Георгия (Аддис-Абеба), Сан-Витале (в городе Равенна, Италия), Замок Кастель-дель-Монте (Апулия, Италия), Флорентийский баптистерий и восьмиугольные церкви Норвегии. Центральное пространство в Ахенский собор, Капелла Карла Великого имеют планы в виде правильного восьмиугольника.

Определение площади сложной фигуры с помощью теории вероятностей

Да мало ли зачем. Например, возникла необходимость определить площадь территории на карте.

Конечно, можно посмотреть в справочнике или поискать в интернете, но иногда и территории бывают нестандартными — допустим, вы озаботились проблемами лесов в пойме Амазонки и хотите ежемесячно измерять площадь зелёных пятен на фотографиях со спутника.

Если вы ботаник (в хорошем смысле слова), то вам может понадобиться измерить площадь листовой поверхности разных сортов одного растения. Или, к примеру, более прозаичная задача — нужно зашпатлевать кусок стены, а банки шпатлёвки хватает только на 1 кв. м. — нужно выяснить, покупать одну банку или раскошелиться на две.

В чём сложность нахождения площади?

Конечно, если фигура представляет собой прямоугольник, круг или, что хуже, эллипс, то проблема решается с помощью Google и калькулятора. Но где бы найти формулу, да попроще, для нахождения площади, скажем, такого рисунка?

Теория вероятностей, Ваш выход!

Сразу оговорюсь, что теория вероятностей по своей сути не подразумевает точного решения задач. Так будет и в этом случае — если вам нужна космическая точность, то предлагаю копать в сторону методов имитационного моделирования. Если же погрешность в пределах 2-5% вас вполне устраивает, то будет достаточно того же калькулятора, базовых навыков программирования и умения считать до ста.

Суть метода

Суть метода проста до банальности. Допустим, мы пасмурным деньком выложили капустный листочек (см. ремарку про биолога выше) на прямоугольный поддон, а поддон выставили под накрапывающий дождик.

А потом засекли определённое время (к примеру, пять минут) и посчитали, сколько капелек упало на поддон, а сколько непосредственно на лист.

Если принять во внимание, что дождь обычно капает равномерно, то получается простая пропорция — лист во столько раз меньше поддона, во сколько раз на него упало меньше капель дождя, чем на весь поддон

Возвращаемся к нашей фигуре

Итак, как же определить площадь той розовой пятерни? Да очень просто — заключить фигуру в прямоугольные границы и проставить случайным образом много точек. Чем больше, тем лучше (в соответствии с законом больших чисел). А потом подсчитать количество точек, попавших на фигуру.

Я намеренно не обсуждаю вопросы реализации такого алгоритма, потому что вариантов масса. Можно просто закрыть глаза и наугад тыкать шариковой ручкой, а можно действовать более научно — с помощью языков программирования.

Например, код на PHP занял у меня не больше 15 строчек, а в результате получилось вот что: Точки общим числом 300, разумеется, проставлены с помощью генератора случайных чисел.

Для удобства подсчета точек я разбил изображение на 36 секторов — теперь нужно подсчитать количество точек, попавших на изображение, в каждом секторе, а результаты сложить.

Сведём данные в таблицу (ячейка таблицы соответствует сектору на картинке):

4	8	4
7	5	6	4
3	6	13	7	8	5
1	10	10	13	7	2
2	3	7	10	2
2	5	3

Теперь у нас есть все данные для того, чтобы вычислить площадь розовой пятерни: площадь описанного прямоугольника — 20 см х 20 см = 400 кв. см; количество точек в прямоугольнике — 300; количество точек внутри фигуры (сумма значений из таблицы) — 157;

площадь фигуры – 209,33 кв. см.

И насколько это точно?

Действительно, осталось определиться с точностью данного метода. Конечно, всё зависит от количества точек, и здесь нужно соблюдать золотую середину — десяти для нашего примера было бы явно недостаточно, а от тысячи слишком рябило бы в глазах. Поэтому попробуем определить погрешность для трёхсот точек и описанного квадрата со стороной 20 см.

Для этого возьмём фигуру, площадь которой нам известна заранее.

Например, такую: Проставляем точки: Результаты заносим в таблицу:

6	11	8	5
9	15	8	5	13	2
11	8	5	14	13	5
10	11	8	8	4	4
2	14	9	10	4	1
3	5	6

Рассчитываем площадь фигуры: площадь описанного прямоугольника — 20 см х 20 см = 400 кв. см; количество точек в прямоугольнике — 300; количество точек внутри фигуры (сумма значений из таблицы) — 237;

площадь фигуры – 316 кв. см.

Нетрудно посчитать, что реальная площадь круга с радиусом 10 см составляет 314,16 кв. см. Таким образом, погрешность метода составила 0,59%, чего в большинстве случаев достаточно для прикладного использования.

• теория вероятностей
• площадь фигуры

Хабы:

Инструкция

Внимательно прочитайте условие поставленной задачи. Руководствуясь им, нарисуйте на листе бумаги предполагаемый пятиугольник.

Обозначьте длину каждой из его сторон.

Проведите в пятиугольнике две диагонали. Обозначьте длину каждой диагонали.

Обратите внимание на то, что получилось в результате проведения диагоналей, и вы увидите, что они разбивают пятиугольник на три различных между собой треугольника. Из вершины каждого треугольника проведите высоту к его основанию. Из вершины каждого треугольника проведите высоту к его основанию

Из вершины каждого треугольника проведите высоту к его основанию.

Измерьте длину высоты опущенной на основание для каждого треугольника.

Определите всех трех треугольников по формуле, приведенной ниже:S = 1/2 x H x a,где S – вычисляемая площадь треугольника;H – высота каждого треугольника;a – длина основания треугольника.

Вычислите площадь пятиугольника, сложив площади этих трех треугольников.

Обратите внимание

Помните, что правильным считается тот пятиугольник, у которого и все стороны, и все углы равны между собой. Если хотя бы одна сторона или угол отличается от других, то пятиугольник не считается правильным, и его площадь нельзя рассчитывать по упрощенной схеме.

Полезный совет

Проще всего определить площадь правильного пятиугольника. Для этого достаточно просто вычислить площадь одного из треугольников, а затем умножить ее на их количество. Ведь диагонали в правильном пятиугольнике разбивают его на треугольники одинаковой площади. Значительно упрощается задача и в том случае, если два угла пятиугольника являются прямыми. Достаточно провести одну диагональ, которая разобьет пятиугольник на треугольник и прямоугольник, площади которых можно найти совсем просто. Сумма вычисленных площадей будет равна площади самого пятиугольника.

Многоугольник или полигон — геометрическая фигура, которая имеет n-ное количество углов. В общем случае многоугольник — это часть плоскости, которая ограничена замкнутой ломанной.

Площадь многоугольника

Расчет площади многоугольника по введенным сторонами и диагоналям, разбивающим многоугольник на непересекающиеся треугольники

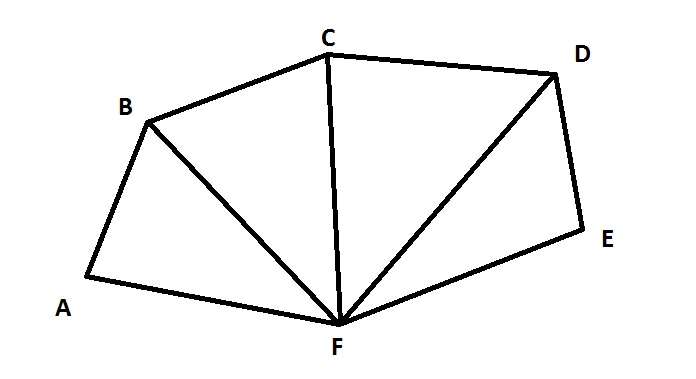
Данный калькулятор обсчитывает площадь многоугольника по введенным сторонами и диагоналям, разбивающим многоугольник на непересекающиеся треугольники.

Смотрим на картинку — площадь многоугольника ABCDE можно вычислить как сумму площадей треугольников ABD, BCD и ADE. Для этого, понятно, помимо длин сторон многоугольника, надо знать еще и длины диагоналей BD и AD, но это и все что нужно — площадь любого треугольника можно вычислить только по длинам его сторон, без измерения углов.

А это довольно удобно, например, при бытовом ремонте — длины-то всяко проще померять, чем углы.

Итак, измеряем длины сторон интересующего нас многоугольника, заносим их в таблицу, мысленно разбиваем многоугольник на треугольники, измеряем нужные диагонали, также заносим их в таблицу, после чего калькулятор рассчитывает площадь всей фигуры. Для проверки также выводятся площади обсчитанных им треугольников. В поле «Ошибка» выводится вершина, которую не удалось сопоставить ни одному треугольнику (если, например, введены еще не все диагонали).

По умолчанию в таблицу введены стороны и диагонали многоугольника на картинке, что легко исправить, нажав кнопку «Очистить таблицу».

Источник

Геометрия многоугольников

В целом такая геометрическая фигура может иметь абсолютно любой вид. К примеру, символы звезды и компаса, полигон для моделирования или грань шестеренки — многоугольники. Многоугольные фигуры разделяются на две группы:

• невыпуклые, которые имеют любую причудливую форму с возможными самопересечениями (самый очевидный пример — звезда);
• выпуклые, все точки которых находятся по одну сторону от прямой, проведенной через две соседние вершины (квадрат, треугольник).

Выпуклый полигон, у которого все углы равны и все стороны равны, считается правильным и имеет собственное название. К примеру, правильный пятиугольник называется пентагон, шести — гексагон, восьмиугольник — октагон, десятиугольник — декагон, одиннадцатиугольник — гендекагон, двенадцати — додекагон. Любой правильный многоугольник имеет свою вписанную и описанную окружность. При этом круг также можно представить как правильный полигон, который имеет бесконечное количество углов.

Немного теории о многоугольниках

Если провести три или более пересекающихся прямых, то они образуют некоторую фигуру. Именно она является многоугольником. По количеству точек пересечения становится ясно, сколько вершин у него будет. Они дают название получившейся фигуре. Это может быть:

• треугольник;
• четырехугольник;
• пяти- или шестиугольник и так далее.

Такая фигура непременно будет характеризоваться двумя положениями:

1. Смежные стороны не принадлежат одной прямой.
2. У несмежных отсутствуют общие точки, то есть они не пересекаются.

Чтобы понять, какие вершины являются соседними, потребуется посмотреть, принадлежат ли они одной стороне. Если да, то соседние. В противном случае их можно будет соединить отрезком, который необходимо назвать диагональю. Их можно провести только в многоугольниках, у которых больше трех вершин.

Совет по решению задачи, для которой многоугольник изображен на бумаге в клетку

Чаще всего озадачивает то, что в данных имеется только размер клеточки. Но оказывается, что больше сведений не нужно. Рекомендацией к решению такой задачи является разбивание фигуры на множество треугольников и прямоугольников. Их площади довольно просто сосчитать по длинам сторон, которые потом легко сложить.

Но часто есть более простой подход. Он заключается в том, чтобы дорисовать фигуру до прямоугольника и вычислить значение его площади. Потом сосчитать площади тех элементов, которые оказались лишними. Вычесть их из общего значения. Этот вариант порой предполагает несколько меньшее число действий.

Как найти площадь неправильной фигуры | Сделай все сам

В школьном курсе геометрии ученики в основном считают площади положительных многоугольников. Между тем, для решения множества фактических задач неоднократно доводится иметь дело с неправильными геометрическими фигурами.

С этой задачей человек сталкивается и при определении размеров дачного участка либо придомовой территории, и при расчете числа ткани для шитья, и еще во многих случаях.

Высчитать площадь неправильной фигуры дозволено несколькими методами.

Вам понадобится

• – неправильная геометрическая фигура;
• – измерительные инструменты;
• – прозрачный пластик;
• – линейка;
• – угольник;
• – шариковая ручка.

Инструкция

1. Разглядите геометрическую фигуру и определите, какие ее параметры вам вестимы. Это могут быть длины сторон либо углы. В зависимости от заданных параметров и выберите метод определения площади. Скажем, поделите ее на несколько фигур, формулы вычисления площади которых вы знаете.

Один из самых распространенных способов — провести диагонали из одного угла ко каждым остальным вершинам. В этом случае вам необходимо знать формулу вычисления площади произвольного треугольника. Но никто не воспрещает поделить заданную фигуру и на другие многоугольники.

Скажем, при расчете площади пола в комнате с нишей комфортнее поделить неправильную фигуру на два прямоугольника либо квадрата.

2. Для определения площади не слишком огромный детали дозволено воспользуйтесь палеткой. Ее дозволено сделать самому. Отрежьте прямоугольный кусок всякого прозрачного пластика.

Поделите его на квадраты, площадь которых вам вестима — скажем, 1х1 либо 0,5х0,5 см. Линейка и угольник обязаны быть точными. Наложите палетку на деталь. Сосчитайте полные квадратики, после этого — неполные.

Роль палетки будет исполнять сетка из квадратов со стороной 1х1 м, начерченная на земле либо подмеченная колышками с протянутыми между ними шнурами. Дозволено ограничиться и разметкой территории на полосы. .

3. С большими площадями дозволено поступить и напротив. Возьмите максимально точный план участка либо придомовой территории. Определите масштаб. Воспользуйтесь одним из предложенных методов. После этого полученное число квадратных сантиметров переведите в надобный масштаб.

Перед тем как начинать ремонт пола в доме, нужно узнать всеобщую площадь , дабы верно рассчитать число материала. Несложная, казалось бы, задача на деле может вызвать много сложностей. Дабы положительно обнаружить площадьпола , вам нужно знать некоторые нюансы измерительной науки.

Вам понадобится

• – рулетка;
• – электронный дальномер;
• – лист бумаги и карандаш;
• – калькулятор.

Площадь многоугольника

Площадь геометрической фигуры — это характеристика плоского объекта, которая показывает его размер. Площадь невыпуклых многоугольников находится путем разбиения фигуры на более мелкие составляющие, обычно треугольники или квадраты. Наш онлайн-калькулятор позволяет вычислять площадь только правильных многоугольников, которая определяется общей формулой:

S = n/4 × a^2 × ctg(pi/n),

где n — количество сторон фигуры, a — длина стороны.

Подставляя вместо n количество сторон фигуры можно получить формулу для определения площади любого правильного полигона, которая будет представлять собой площадь квадрата a^2, умноженного на определенный коэффициент. Интересно, что при увеличении количества углов этот коэффициент также будет увеличиваться, к примеру, для пентагона — 1,72, а гексагона — 2,59.

Так как около любого правильного полигона можно описать окружность или вписать ее в него, мы можем использовать соответствующие радиусы для вычисления площадей многоугольников. Сторона и радиус описанной окружности для любого полигона соотносятся как:

a = R × 2 sin (pi/n),

где R – радиус описанной окружности, n – количество сторон геометрической фигуры.

Для вписанной в полигон окружности соотношение немного изменяется и выглядит как:

a = r × 2 tg (pi/n),

где r – радиус вписанной окружности.

Таким образом, для определения площади любого правильного полигона вам понадобится указать количество сторон n и любой параметр на выбор:

• длина стороны a;
• радиус вписанной окружности r;
• радиус описанной окружности R.

Рассмотрим пару примеров для нахождения площади любого многоугольника.