Как определить площадь четырехугольника

Диагонали

Свойства диагоналей в четырехугольниках

В следующей таблице указано, пересекают ли диагонали некоторых основных четырехугольников пополам, перпендикулярны ли их диагонали и равны ли их диагонали. Список применяется к наиболее общим случаям и исключает названные подмножества.

Четырехугольник	Деление диагоналей пополам	Перпендикулярные диагонали	Равные диагонали
Трапеция	Нет	См. Примечание 1	Нет
Равнобедренная трапеция	Нет	См. Примечание 1	да
Параллелограмм	да	Нет	Нет
летающий змей	См. Примечание 2	да	См. Примечание 2
Прямоугольник	да	Нет	да
Ромб	да	да	Нет
Квадратный	да	да	да

Примечание 1: самые общие трапеции и равнобедренные трапеции не имеют перпендикулярных диагоналей, но существует бесконечное количество (непохожих) трапеций и равнобедренных трапеций, которые имеют перпендикулярные диагонали и не являются никакими другими именованными четырехугольниками.

Примечание 2: В кайте одна диагональ делит другую пополам. Самый общий воздушный змей имеет неравные диагонали, но существует бесконечное количество (не похожих) воздушных змеев, в которых диагонали равны по длине (и воздушные змеи не являются никакими другими названными четырехугольниками).

Длины диагоналей

Длины диагоналей выпуклого четырехугольника ABCD можно вычислить, используя закон косинусов для каждого треугольника, образованного одной диагональю и двумя сторонами четырехугольника. Таким образом

пзнак равноа2+б2-2абпотому что⁡Bзнак равноc2+d2-2cdпотому что⁡D{\ displaystyle p = {\ sqrt {a ^ {2} + b ^ {2} -2ab \ cos {B}}} = {\ sqrt {c ^ {2} + d ^ {2} -2cd \ cos { D}}}}

а также

qзнак равноа2+d2-2аdпотому что⁡Азнак равноб2+c2-2бcпотому что⁡C.{\ displaystyle q = {\ sqrt {a ^ {2} + d ^ {2} -2ad \ cos {A}}} = {\ sqrt {b ^ {2} + c ^ {2} -2bc \ cos { C}}}.}

Другие, более симметричные формулы для длин диагоналей:

пзнак равно(аc+бd)(аd+бc)-2абcd(потому что⁡B+потому что⁡D)аб+cd{\ displaystyle p = {\ sqrt {\ frac {(ac + bd) (ad + bc) -2abcd (\ cos {B} + \ cos {D})} {ab + cd}}}}

а также

qзнак равно(аб+cd)(аc+бd)-2абcd(потому что⁡А+потому что⁡C)аd+бc.{\ displaystyle q = {\ sqrt {\ frac {(ab + cd) (ac + bd) -2abcd (\ cos {A} + \ cos {C})} {ad + bc}}}.}

Обобщения закона параллелограмма и теоремы Птолемея

В любом выпуклом четырехугольнике ABCD сумма квадратов четырех сторон равна сумме квадратов двух диагоналей плюс четыре квадрата отрезка прямой, соединяющего середины диагоналей. Таким образом

а2+б2+c2+d2знак равноп2+q2+4Икс2{\ displaystyle a ^ {2} + b ^ {2} + c ^ {2} + d ^ {2} = p ^ {2} + q ^ {2} + 4x ^ {2}}

где x — расстояние между серединами диагоналей. Это иногда называют теоремой Эйлера о четырехугольнике и является обобщением закона параллелограмма .

Немецкий математик Карл Антон Бретшнайдер вывел в 1842 году следующее обобщение теоремы Птолемея , касающееся произведения диагоналей в выпуклом четырехугольнике.

п2q2знак равноа2c2+б2d2-2абcdпотому что⁡(А+C).{\ displaystyle p ^ {2} q ^ {2} = a ^ {2} c ^ {2} + b ^ {2} d ^ {2} -2abcd \ cos {(A + C)}.}

Это соотношение можно рассматривать как закон косинусов для четырехугольника. В круговом четырехугольнике , где A + C = 180 °, он сводится к pq = ac + bd . Поскольку cos ( A + C ) ≥ −1, это также дает доказательство неравенства Птолемея.

Другие метрические отношения

Если X и Y являются основаниями нормалей из B и D к диагонали AC = p в выпуклом четырехугольнике ABCD со сторонами a = AB , b = BC , c = CD , d = DA , то

ИксYзнак равно|а2+c2-б2-d2|2п.{\ displaystyle XY = {\ frac {| a ^ {2} + c ^ {2} -b ^ {2} -d ^ {2} |} {2p}}.}

В выпуклый четырехугольник ABCD со сторонами = АВ , Ь = БК , гр = CD , д = DA , и где диагонали пересекаются в точке Е ,

ежграммчас(а+c+б+d)(а+c-б-d)знак равно(аграммчас+cеж+бечас+dжграмм)(аграммчас+cеж-бечас-dжграмм){\ displaystyle efgh (a + c + b + d) (a + cbd) = (agh + cef + beh + dfg) (agh + cef-beh-dfg)}

где e = AE , f = BE , g = CE и h = DE .

Форма и размер выпуклого четырехугольника полностью определяются длиной его сторон в последовательности и одной диагонали между двумя заданными вершинами. Две диагонали p, q и четыре стороны a, b, c, d четырехугольника связаны определителем следующим образом:

Detа2п2d21а2б2q21п2б2c21d2q2c211111знак равно{\ displaystyle \ det {\ begin {bmatrix} 0 & a ^ {2} & p ^ {2} & d ^ {2} & 1 \\ a ^ {2} & 0 & b ^ {2} & q ^ {2} & 1 \\ p ^ { 2} & b ^ {2} & 0 & c ^ {2} & 1 \\ d ^ {2} & q ^ {2} & c ^ {2} & 0 & 1 \\ 1 & 1 & 1 & 1 & 0 \ end {bmatrix}} = 0.}

Калькулятор расчета площади земельного участка неправильной формы

Инструкция для калькулятора расчета площади неправильного земельного участка

Данный онлайн калькулятор помогает произвести расчет, определение и вычисление площади земельного участка в онлайн режиме. Представленная программа способна правильно подсказать, как выполнить расчет площади земельных участков неправильной формы.

Указываем все данные в метрах

A B, D A, C D, B C— Размер каждой стороны делянки.

Согласно введен данным, наша программа в онлайн режиме выполнить расчет и определить, площадь земельных угодий в квадратных метрах, сотках, акрах и гектарах.

Методика определения размеров участка ручным методом

Чтобы правильно выполнить расчет площади делянок, не нужно использовать сложные инструменты. Мы берем деревянные колышки или металлические прутья и устанавливаем их в углах нашего участка. Далее при помощи измерительной рулетки определяем ширину и длину делянки. Как правило, достаточно выполнить замер одной ширины и одной длины, для прямоугольных или равносторонних участков. Для примера, у нас получились следующие данные: ширина – 20 метров и длина – 40 метров.

Далее переходим к расчету площади делянки. При правильной форме участка, можно использовать геометрическую формулу определения площади (S) прямоугольника. Согласно этой формуле, нужно выполнить умножение ширины (20) на длину (40) , то есть произведение длин двух сторон. В нашем случае S=800 м².

После того, как мы определили нашу площадь, мы можем определить количество соток на земельном участке. Согласно общепринятым данным, в одной сотке – 100 м². Далее при помощи простой арифметики, мы разделим наш параметр S на 100. Готовый результат и станет равен размеру делянки в сотках. Для нашего примера, этот результат – 8. Таким образом, получаем, что площадь участка составляет восемь соток.

В том случае, когда территория угодий очень большая, то лучше всего выполнять все измерения в других единицах – в гектарах. Согласно общепринятым единицам измерения – 1 Га = 100 соток. К примеру, если наша земельная делянка согласно полученным измерениям составляем 10 000 м², то в этом случае его площадь равна 1 гектару или 100 соткам.

Если Ваш участок неправильной формы, то в этом случае количество соток напрямую зависит от площади. Именно по этой причине при помощи онлайн калькулятора Вы сможете правильно рассчитать параметр S делянки, и после этого разделив полученный результат на 100. Таким образом, Вы получите расчеты в сотках. Такой метод предоставляет возможность измерять делянки сложных форм, что весьма удобно.

Общие данные

Расчет площади земельных участков базируется на классических расчетах, которые выполняются согласно общепринятым геодезическим формулам.

Всего доступно несколько методов для расчета площади земельных угодий – механический (рассчитывается по плану при помощи мерных палеток), графический (определяется по проекту) и аналитический (при помощи формулы площади по измеренным линиям границ).

На сегодняшний день самым точным способом заслуженно считается – аналитический. Используя данный метод, ошибки при расчетах, как правило, появляются из-за погрешностей на местности измеренных линий. Данный способ является также и достаточно сложным, если границы криволинейные или количество углом на делянке больше десяти.

Немного проще по расчетам является графическим способ. Его лучше всего использовать в том случае, когда границы участка представлены в виде ломанной линии, с небольшим количеством поворотов.

И самый доступный и простой способ, и наиболее популярный, но и в тоже время самой большой погрешностью – механический способ. Используя данный метод, Вы сможете легко и быстро выполнить расчет площади земельных угодий простой или сложной формы.

Среди серьезных недостатков механического или графического способа, выделяют следующее, кроме погрешностей при измерении участка, при расчетах добавляется погрешность из-за деформации бумаги или погрешность при составлении планов.

Источник

Замечательные точки и прямые в выпуклом четырехугольнике

Центр четырехугольника можно определить несколькими способами. «Центроид вершины» получается из рассмотрения четырехугольника как пустого, но с равными массами в вершинах. «Боковой центроид» исходит из рассмотрения сторон, имеющих постоянную массу на единицу длины. Обычный центр, называемый просто центроидом (центром площади), происходит от рассмотрения поверхности четырехугольника как имеющей постоянную плотность. Эти три точки, как правило, не одно и то же.

«Центроид вершины» — это пересечение двух . Как и в случае любого многоугольника, координаты x и y центроида вершины являются средними арифметическими значениями x и y координат вершин.

«Центроид площади» четырехугольника ABCD можно построить следующим образом. Пусть G _a , G _b , G _c , G _d — центроиды треугольников BCD , ACD , ABD , ABC соответственно. Тогда «центроид площади» — это пересечение прямых G _a G _c и G _b G _d .

В общем выпуклом четырехугольнике ABCD , нет никаких природных аналогий к описанной окружности и ортоцентру в виде треугольника . Но две такие точки можно построить следующим образом. Пусть O _a , O _b , O _c , O _d — центры описанной окружности треугольников BCD , ACD , ABD , ABC соответственно; и обозначим через H _a , H _b , H _c , H _d ортоцентры в тех же треугольниках. Тогда пересечение прямых O _a O _c и O _b O _d называется квазиокружностью центра , а пересечение прямых H _a H _c и H _b H _d называется квазиортоцентром выпуклого четырехугольника. Эти точки можно использовать для определения линии Эйлера четырехугольника. В выпуклом четырехугольнике, в quasiorthocenter Н , «площадь центра тяжести» G и quasicircumcenter вывод является коллинеарен в этом порядке, и HG = 2 GO .

Также можно определить квазининоточечный центр E как пересечение прямых E _a E _c и E _b E _d , где E _a , E _b , E _c , E _d — центры девяти точек треугольников BCD , ACD. , ABD , ABC соответственно. Тогда Е является средней точкой из ОН .

Еще одна замечательная линия в выпуклом четырехугольнике без параллелограмма — это линия Ньютона , которая соединяет середины диагоналей, причем отрезок, соединяющий эти точки, делится пополам центром тяжести вершины. Еще одна интересная линия (в некотором смысле двойственная линии Ньютона ) — это линия, соединяющая точку пересечения диагоналей с центром тяжести вершины. Эта линия примечательна тем, что содержит центр тяжести (площади). Центроид вершины делит отрезок, соединяющий точку пересечения диагоналей и центр тяжести (площади) в соотношении 3: 1.

Для любого четырехугольника ABCD с точками P и Q пересечения AD и до н.э. и AB и CD , соответственно, круги (PAB), (PCD), (QAD), и (QBC) проходят через общую точку М , называется Микель точка.

Для выпуклого четырехугольника ABCD, в котором E — точка пересечения диагоналей, а F — точка пересечения продолжений сторон BC и AD , пусть ω — окружность, проходящая через E и F, которая пересекает CB внутренне в M и DA внутренне. на N . Пусть CA встретиться снова на Q , L , и пусть DB встретиться снова на Q , K . Тогда верно: прямые NK и ML пересекаются в точке P, которая находится на стороне AB ; прямые NL и KM пересекаются в точке Q , расположенной на стороне CD . Точки P и Q называются «точками Паскаля», образованными окружностью ω на сторонах AB и CD .

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия

В данном разделе рассматриваются только выпуклые фигуры, и считается известной формула:

которая позволяет найти площадь прямоугольникапрямоугольника с основанием a и высотой b.

Формулы для площадей четырехугольников

Четырехугольник	Рисунок	Формула площади	Обозначения
Прямоугольник		S = ab

Посмотреть вывод формулы

d – диагональ,φ – любой из четырёх углов между диагоналями

Получается из верхней формулы подстановкой d=2R

R – радиус описанной окружности,φ – любой из четырёх углов между диагоналями

Параллелограмм

Посмотреть вывод формулы

a – сторона,h_a – высота, опущенная на эту сторону

Посмотреть вывод формулы

a и b – смежные стороны,φ – угол между ними

Посмотреть вывод формулы

φ – любой из четырёх углов между ними

Квадрат

S = a 2

a – сторона квадрата

S = 4r 2

r – радиус вписанной окружности

Посмотреть вывод формулы

d – диагональ квадрата

Получается из верхней формулы подстановкой d = 2R

R – радиус описанной окружности

Ромб

Посмотреть вывод формулы

a – сторона,h_a – высота, опущенная на эту сторону

Посмотреть вывод формулы

a – сторона,φ – любой из четырёх углов ромба

Посмотреть вывод формулы

Посмотреть вывод формулы

a – сторона,r – радиус вписанной окружности

Посмотреть вывод формулы

r – радиус вписанной окружности,φ – любой из четырёх углов ромба

Трапеция

Посмотреть вывод формулы

a и b – основания,h – высота

S = m h

m – средняя линия,h – высота

Посмотреть вывод формулы

φ – любой из четырёх углов между ними

Посмотреть вывод формулы

a и b – основания,c и d – боковые стороны

Дельтоид

S = ab sin φ

a и b – неравные стороны,φ – угол между ними

a и b – неравные стороны,φ₁ – угол между сторонами, равными a ,φ₂ – угол между сторонами, равными b.

Посмотреть вывод формулы

a и b – неравные стороны,r – радиус вписанной окружности

Посмотреть вывод формулы

Произвольный выпуклый четырёхугольник

Посмотреть вывод формулы

φ – любой из четырёх углов между ними

Вписанный четырёхугольник

,

Посмотреть вывод формулы Брахмагупты

a, b, c, d – длины сторон четырёхугольника,p – полупериметр,

Формулу называют «Формула Брахмагупты»

Прямоугольник

гдеa и b – смежные стороны

гдеd – диагональ,φ – любой из четырёх углов между диагоналями

Посмотреть вывод формулы

гдеR – радиус описанной окружности,φ – любой из четырёх углов между диагоналями

Формула получается из верхней формулы подстановкой d = 2R

Параллелограмм

гдеa – сторона,h_a – высота, опущенная на эту сторону

Посмотреть вывод формулы

гдеa и b – смежные стороны,φ – угол между ними

Посмотреть вывод формулы

φ – любой из четырёх углов между ними

Посмотреть вывод формулы

Квадрат

S = a 2

гдеa – сторона квадрата

S = 4r 2

гдеr – радиус вписанной окружности

гдеd – диагональ квадрата

Посмотреть вывод формулы

гдеR – радиус описанной окружности

Получается из верхней формулы подстановкой d = 2R

Ромб

гдеa – сторона,h_a – высота, опущенная на эту сторону

Посмотреть вывод формулы

гдеa – сторона,φ – любой из четырёх углов ромба

Посмотреть вывод формулы

Посмотреть вывод формулы

гдеa – сторона,r – радиус вписанной окружности

Посмотреть вывод формулы

гдеr – радиус вписанной окружности,φ – любой из четырёх углов ромба

Посмотреть вывод формулы

Трапеция

гдеa и b – основания,h – высота

Посмотреть вывод формулы

гдеm – средняя линия,h – высота

φ – любой из четырёх углов между ними

Посмотреть вывод формулы

гдеa и b – основания,c и d – боковые стороны

Посмотреть вывод формулы

Дельтоид

гдеa и b – неравные стороны,φ – угол между ними

гдеa и b – неравные стороны,φ₁ – угол между сторонами, равными a ,φ₂ – угол между сторонами, равными b.

гдеa и b – неравные стороны,r – радиус вписанной окружности

Посмотреть вывод формулы

Посмотреть вывод формулы

Произвольный выпуклый четырёхугольник

φ – любой из четырёх углов между ними

Посмотреть вывод формулы

Вписанный четырёхугольник

,

гдеa, b, c, d – длины сторон четырёхугольника,p – полупериметр

Формулу называют «Формула Брахмагупты»

Посмотреть вывод формулы Брахмагупты

Формулы вычисления площади произвольного четырёхугольника

В школьных математических заданиях часто требуется определить площадь четырёхугольника.

Ниже мы изучим различные методы расчётов площади произвольных четырёхугольников, запишем формулы и рассмотрим различные вспомогательные примеры. В приведённой ниже таблице будут указаны определения и договорённости, которые будут использоваться в дальнейшем во время наших рассуждений.

• Вписанная окружность — это окружность, которая касается всех сторон многоугольника. В дальнейшем в статье для обозначения её радиуса будем использовать латинскую букву r.
• Описанная окружность — это окружность, которой принадлежат все вершины многоугольника ( её радиуса обозается буквой R).
• Угол между сторонами a и b будем обозначать следующей записью (a,b).
• Синус угла — это число равное отношению противоположного катета к гипотенузе в прямоугольном треугольнике. (её обозначение – запись sin).
• Диагональ — отрезок, соединяющий вершины многоугольника не лежащие на одной стороне (её обозначение – латинская буква d).
• Четырёхугольник — это фигура из четырёх точек (вершин), из которых любые три не лежат на одной прямой, и четырёх отрезков (сторон) последовательно их соединяющих.
• Площадь фигуры — это численное значение территории, заключённой внутри многоугольника (её обозначение – латинская буква S).
• Косинус угла — это число равное отношению прилежащего катета к гипотенузе в прямоугольном треугольнике. В дальнейшем в статье для его обозначения будем использовать латинскую запись cos.

Узнаем как найти площадь четырёхугольника когда даны его диагонали и образуемый при их пересечении острый угол. Тогда площадь четырёхугольника будет вычисляться по формуле: S = 1/2*d1*d2*sin(d1,d2). Рассмотрим пример.

Методика выполнения работы

Перед тем, как рассчитать квадратуру дома, нужно подготовить следующее:

1. Калькулятор для проведения вычислений. 
2. Рулетка для проведения измерений. При этом надо учитывать, что некоторые производят измерения в дюймах – они не подойдут. Нужна рулетка, которая указывает длину с помощью сантиметров. 
3. Потребуется план квартиры. Измерение площади стен, пола и потолка будет выполняться на его основе. Если такую схему найти нельзя, то её нужно нарисовать от руки, стремясь реалистично отобразить размеры и геометрическую форму частей. 
4. Также потребуется бумага и карандаш для ведения записей в процессе работы. 

При замерах полов, стен и потолков в первую очередь потребуются знания из школьной геометрии. Простейшим способом, как рассчитать площадь дома в квадратных метрах, является вычисление прямоугольных поверхностей. Площадь прямоугольника вычисляется как произведение его сторон. 

Вычисление площади простейших геометрических фигур основано на базовых формулах из геометрииИсточник stroychik.ru

При этом важно учитывать следующее.

Хотя на вид комната состоит из прямоугольных деталей, на самом деле это может оказаться немного по-другому. Например, ширина стен, измеренная с одной и другой стороны, может отличаться на несколько сантиметров. Эта проблема особенно существенна при измерении расстояний в домах старой постройки. В таких случаях обычно измеряют длину в нескольких местах, а при вычислении площади используют среднее значение. 
Вычисления позволяют получить нужные цифры с высокой точностью

Однако будет разумной предосторожностью при вычислениях добавить к площади небольшую величину. Это позволит исключить ситуацию, в которой стройматериалов чуть-чуть не хватило. 

Таким способом можно вычислить площадь прямоугольных пустых стен, пола и потолка.
 

Сложная форма стен и потолка может быть разделена на простые фигуры для упрощения вычисленийИсточник www.buvbaze.lv

Расчёт площади стен с окнами и дверьми

Если на стене есть окно или дверь, то вычисление производится следующим образом:

• Определяется площадь стены без учёта двери или окна. 
• Вычисляется площадь каждого окна или двери путём умножения их длины на ширину. 
• Из площади стены вычитают площадь окон и дверей. 

Этот способ применим в тех случаях, когда рассматриваются прямоугольные стены.

Площадь стены, имеющей неправильную форму

В этом случае нужно разделить вычисления на этапы. Стена с нишами может иметь сложную форму. Однако её всегда можно условно разбить на несколько участков, каждый из которых соответствует одной из простых форм. Затем надо рассчитать площади каждой из частей и сложить их. 

Как посчитать площадь стен, рассказано в видео

Расчёт через периметр

Если комната имеет неправильную форму, то площадь стен можно вычислить, измерив длину периметра. В этом случае проводят измерение горизонтальных отрезков по каждой из сторон помещения и складывают их вместе, затем определяют высоту. Произведение этих величин равно площади стен в этом помещении. 

Несколько советов

• Нужно при проведении расчётов все цифры наносить на план. Таким образом сохранится не только результат, но и промежуточные вычисления, которые могут пригодится при проведении ремонтных работ в будущем. 
• При вычислении площади нужно учитывать, что не всегда необходима полная величина. Например, обои могут клеить не только на всю стену, а на их часть. Класть плитку могут до потолка либо только до определённой высоты. Поэтому нужно точно определить, как высчитать квадратуру дома с учётом конкретного плана ремонта. 

Как сделать замеры – можно посмотреть в видеоролике:

Для того, чтобы точно знать, сколько необходимо стройматериалов для проведения работ, нужно учитывать площади стен, пола и потолка, а также нормы расхода стройматериалов. Среднюю величину расхода можно узнать, спросив у продавцов, а квадратуру дома необходимо измерить самостоятельно. Для этого нужно воспользоваться знаниями из элементарной геометрии. При вычислении площади сложных фигурных поверхностей их разбивают на простые части, делают необходимые вычисления, затем суммируют их. 

Информация о прямоугольнике

Прямоугольник — четырехугольная геометрическая фигура, противолежащие стороны которой равны и углы являются прямыми. Частным случаем данной фигуры считается квадрат. У него все углы прямые, а также все стороны равны между собой. Для выполнения расчетов нужно знать основные соотношения, свойства и признаки.

Важным аспектом является идентификация фигуры и применение к ней формул и соотношений. В двухмерной геометрии, которую еще называют эвклидовой, можно встретить необычный признак, позволяющий определить принадлежность четырехугольника к прямоугольнику. Его формулировка следующая: достаточно хотя бы трех углов, равных 90 градусам, чтобы четырехугольник считался прямоугольником.

Утверждение легко доказывается. Это связано с тем, что по теореме о сумме внутренних углов произвольного четырехугольника, составляющей 360 градусов, четвертый угол тоже равен 90. Нужно выполнить следующие расчеты для определения градусной меры четвертого угла: D = 360 — (90 + 90 + 90) = 90. Необходимо отметить, что смежные с ними углы равны 90.

Свойства и признаки

Очень часто новички путают свойства и признаки фигуры. Однако это совсем различные понятия. Признаками фигуры называются характерные особенности, которые позволяют отнести ее к тому или иному классу. Свойства — совокупность аксиом, позволяющих использовать некоторые данные при решении или доказательстве теорем и тождеств. Прямоугольник обладает следующими признаками:

1. Условие параллельности и равенства противоположных сторон.
2. Наличие четырех прямых углов.
3. Равенство диагоналей.
4. Квадрат диагонали равен суммарному значению квадратов двух сторон, которые не противоположны.
5. Все стороны не равны между собой.

Очень важно уметь различать геометрические фигуры. Поскольку прямоугольник является параллелограммом, то их часто путают. Основное его отличие — это равенство всех углов 90 градусов

У параллелограмма и ромба углы будут равняться 90 в том случае, когда они являются квадратами. Последний отличается от искомой фигуры (прямоугольника) равенством всех сторон. Поскольку прямоугольник является частным случаем параллелограмма, то обладает такими же свойствами:

Основное его отличие — это равенство всех углов 90 градусов. У параллелограмма и ромба углы будут равняться 90 в том случае, когда они являются квадратами. Последний отличается от искомой фигуры (прямоугольника) равенством всех сторон. Поскольку прямоугольник является частным случаем параллелограмма, то обладает такими же свойствами:

1. Углы равны между собой 90 градусов.
2. Противолежащие параллельные стороны равны.
3. Сумма всех внутренних углов составляет 360.
4. Диагональ, проведенная внутри прямоугольника, делит его на два равнозначных треугольника, которые являются равновеликими. Они равны по третьему признаку равенства треугольников (размерности сторон одной фигуры равны значениям сторон другой фигуры).
5. Треугольники, полученные при проведении двух диагоналей, равны по всем признакам (углам и сторонам).
6. Диагонали пересекаются между собой в точке, которая делит их на четыре равные части.
7. Точка пересечения диагоналей — центр симметрии.
8. Сумма квадратов двух диагоналей соответствует суммарному значению квадратов всех сторон фигуры.

Периметр и размерность

Нужно ввести некоторые обозначения. Пусть стороны прямоугольника АВСД обозначаются литерами a и b. Поскольку диагонали равны, то можно только обозначить размерность одной буквой «d». Периметром называется сумма всех сторон заданной фигуры. Он обозначается литерой P. Для его нахождения применяется формула такого вида: P = 2 * (a + b). Однако бывает случай, когда известна только одна его сторона и диагональ. Формула приобретает следующий вид: P = 2a + ^(1/2) и P = 2b + ^(1/2).

Чтобы вычислить площадь прямоугольника, следует воспользоваться таким соотношением: S = a * b. Эта базовая формула, которая используется также в строительной сфере и физике. Однако существует еще один способ, с помощью которого можно узнать площадь прямоугольника. Она находится с помощью формулы Герона для треугольников с площадями S1 и S2, а затем результат умножается на 2. Эта особенность основывается на свойстве фигуры, поскольку диагональ делит его на два равных треугольника.

Соотношение имеет следующий вид: S = S1 + S2 = 2S1= 2 * ^(1/2). Переменная «p» — полупериметр треугольника. Он находится таким методом: p = P / 2 = (a + b + d) / 2.

Примеры решения

Задачи на нахождение площади применяются в нескольких дисциплинах. В геометрии применяются различные комбинации, при которых известны некоторые величины:

1. Две стороны.
2. Одна из сторон и диагональ.
3. Диагональ и разность сторон.

Для расчета расходных материалов и площади поперечного сечения проводника можно всегда измерить стороны прямоугольника. Существует два способа нахождения: автоматизированный и ручной. В первом случае используется специализированное программное обеспечение. Однако вовсе не обязательно применять сложные алгоритмы и программные модули, поскольку формула является очень простой. Для расчета специалисты рекомендуют применять онлайн-калькулятор.

При ручном режиме расчета нужно подставлять значения в формулу. После этого выполнять вычисления. Возможна и оптимизация процесса вычисления. Для этой цели рекомендуется использовать Excel. Приложение входит в состав стандартного офисного пакета MS Office.

Геометрия на плоскости

Задача сводится к тому, что необходимо высчитать S, зная размеры сторон (a = 25 и b = 10). В этом случае следует воспользоваться базовой формулой: S = a * b = 25 * 10 = 250 (ед 2). В ответе указывается условная единица измерения, поскольку явная не указана в условии задачи.

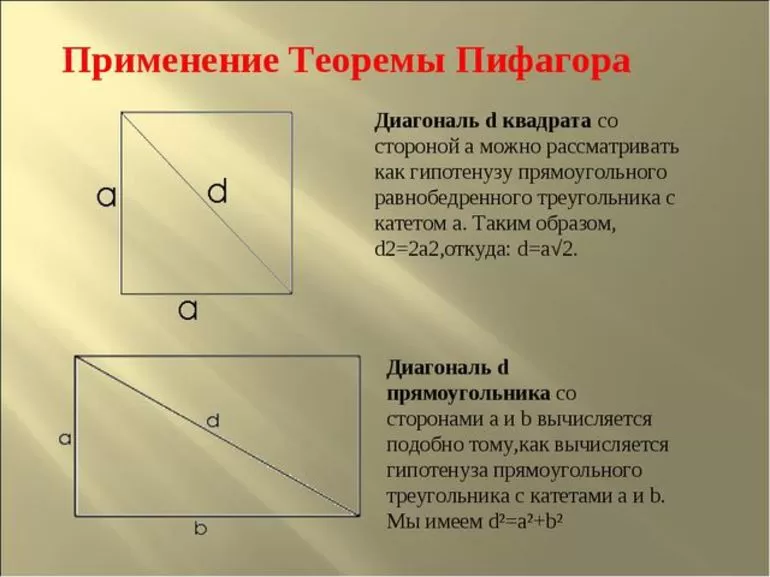
Еще один вариант задания немного сложнее предыдущего. Он имеет следующее условие: одна из сторон прямоугольника равна 6 м и диагональ 10 м. Нужно найти площадь прямоугольника. Формулой в этом случае является теорема Пифагора. Треугольник, который образуется при проведении диагонали, считается прямоугольный (неравносторонний, а разносторонний). Решается задача следующим образом:

1. Находится неизвестная сторона: b =(d 2 — a 2)^(1/2) = (100 — 36)^(1/2) = 8 (м).

2. Площадь (произведение сторон): S = 6 * 8 = 48 (м 2).

Можно использовать двойную формулу Герона, однако метод усложняет вычисления. Для сравнения скорости и объема вычислений следует решить задачу вторым способом:

1. Сторона: b = 8 (м).

2. Значение площади будет вычисляться таким образом: S = 2 * ^(1/2) = 2 * 24 = 48 (м 2).

Второй способ считается неправильным, поскольку необходимо во всех задачах оптимизировать вычисления. Сложным типом задачи, кроме интегрирования, считается нахождение площади, когда неизвестны стороны, а известна только диагональ (10). Известно также, что одна из сторон больше другой на 3 метра. В этом случае надо выражать одну сторону через другую. Алгоритм решения следующий:

1. Обозначить стороны: a = x и b = x — 3.
2. Составить уравнение: x * (x — 3) = 10.

3. Раскрыть скобки: x 2 — 3x — 10 = 0.

4. Нахождение дискриминанта: D = b 2 — 4* a * c = 9 — (4 * 10) < 0.

Электротехника и ремонт

Определение площади поперечного сечения проводника необходимо для вычисления сопротивления. В этом случае нужно измерить длину и толщину формы проводника, а затем перемножить стороны между собой. Если он является полым, то площадь фигуры нужно искать с помощью интеграла. Для разных проводников существуют определенные формулы.

Для вычисления расходных материалов нужно искать площадь потолка, стен, комнат или дома. Распространенный пример подсчета квадратуры керамической плитки для санузла: размер комнаты составляет 2,5х1,5 метра. Для подсчета необходимо воспользоваться формулой определения площади комнаты: S = 2,5 * 1,5 = 3,75 (м 2). Однако берется не исходное значение, а приближенное. Его нужно округлять только в большую сторону, т. е. править 3,75 на значение 4. Следует руководствоваться таким правилом: результат округляется в большую сторону.