Приказ росреестра от 23.10.2020 n п/0393

Показатели отклонения

Существуют показатели вариации, учитывающие все значения величин, а не только наибольшие или наименьшие. Одним из них можно назвать среднее линейное отклонение — показатель, характеризующий меру разброса значений. Сначала требуется определить точку отсчёта разброса. Как правило, ею становится среднее арифметическое значение, входящее в исследование величин. Потом необходимо измерить, отклонение от среднего для каждого значения. Все отклонения вычисляются по модулю и определяется среднее значение уже среди них. Формула для расчёта отклонения:

a = Σ n i=1 (x — x̅) / n, где:

• a — среднее линейное отклонение;
• n — количество значений в исследуемой совокупности;
• x — анализируемый показатель;
• x̅ — среднее значение показателя.

СКО характеризует разброс значений относительно среднего математического ожидания. Оно измеряется в единицах измерения само́й величины. Существует правило, согласно которому для нормально распределённых данных диапазон разброса 997 значений из 1 тыс. составляет три сигмы от средней арифметической, .

Классификация ошибок измерений

_______ Измерения в геодезии рассматриваются с двух точек зрения: количественной, выражающей числовое значение измеренной величины, и качественной, характеризующей ее точность. Из практики известно, что даже при самой тщательной и аккуратной работе многократные (повторные) измерения не дают одинаковых результатов. Это указывает на то, что получаемые результаты не являются точным значением измеряемой величины, а несколько отклоняются от него. Значение отклонения характеризует точность измерений.

_______ При геодезических измерениях неизбежны ошибки. Эти ошибки бывают грубые , систематические и случайные .

_______ К грубым ошибкам относятся просчеты в измерениях по причине невнимательности наблюдателя или неисправности прибора, и они полностью должны быть исключены. Это достигается путем повторного измерения.

_______ Систематические ошибки происходят от известного источника, имеют определенный знак и величину и их можно учесть при измерениях и вычислениях.

_______ Случайные ошибки обусловлены разными причинами и полностью исключить их из измерений нельзя. Поэтому возникают две задачи: как из результатов измерений получить наиболее точную величину и как оценить точность полученных результатов измерений. Эти задачи решаются с помощью теории ошибок измерений _______

_______ В основу теории ошибок положены следующие свойства случайных ошибок : _______ 1. Малые ошибки встречаются чаще, а большие реже. _______ 2. Ошибки не превышают известного предела. _______ 3. Положительные и отрицательные ошибки, одинаковые по абсолютной величине, одинаково часто встречаются. _______ 4. Сумма ошибок, деленная на число измерений, стремится к нулю при большом числе измерений.

_______ По источнику происхождения различают ошибки приборов, внешние и личные. Ошибки приборов обусловлены их несовершенством, например погрешность угла, измеренного теодолитом, неточным приведением в вертикальное положение оси его вращения.

_______ Внешние ошибки происходят из-за влияния внешней среды, в которой протекают измерения, например погрешность в отсчете по нивелирной рейке из-за изменения температуры воздуха на пути светового луча (рефракция) или нагрева нивелира солнечными лучами.

_______ Личные ошибки связаны с особенностями наблюдателя, например, разные наблюдатели по-разному наводят зрительную трубу на визирную цель. Так как грубые погрешности должны быть исключены из результатов измерений, а систематические исключены или ослаблены до минимально допустимого предела, то проектирование измерений с необходимой точностью и оценку результатов выполненных измерений производят, основываясь на свойствах случайных погрешностей.

Погрешность При Межевании Земельных Участков 2020

Тенденция того, что одна ошибка может в будущем привести к трем другим, в рамках современного землеустроения стала нормой, одновременно спровоцировав психоз среди населения, когда землевладелец утратил уверенность в законности своего права и вообще в том, что имеющийся участок действительно принадлежит ему.

Рекомендуем прочесть: Норматив потребления воды на 1 человека без счетчика с 2020 ульяновск

Итогом ее является документальное и практическое определение формы участка, его границ и положения на местности. Ошибки в ходе данных работ и являют собой причинно-следственные основы будущих споров, а подчас и плачевных правовых последствий для потенциального собственника. Так, в методиках проведения межевания и земельном законодательстве присутствует такой термин, как допустимая погрешность.

Коэффициент вариации

Квадратичное отклонение — это абсолютная оценка меры разброса. Для того чтобы сравнить величину разброса с самими значениями величины, необходимо применить относительный показатель — коэффициент вариации:

V = σ / x̅, где σ — стандартное отклонение из выборки, x̅ — среднее арифметическое.

Коэффициент вариации измеряется в процентах. Показатель полезен для сравнивания однородности разных процессов.

Математическое ожидание — среднее значение случайной величины. Для дискретной выборки оно определяется по формуле:

M (X)= Σ ni=1 xi ⋅ pi, где xi — случайные значения, pi — их вероятность.

Дисперсией называется среднее значение квадрата отклонения случайной величины от её математического ожидания:

D (X) = M (X2) — (M (X))2

Для дискретной случайной величины формула приобретает вид:

D (X) = Σ ni=1 xi2 ⋅ pi — M (X)2.

Среднеквадратическое отклонение или стандартный разброс — это корень квадратный из дисперсии, формула которого имеет вид:

σ(X) = √ D (X).

Дисперсия и стандартный разброс — взаимозависимые характеристики. Стандартная ошибка среднего — величина, которая характеризует квадратическое отклонение выборочного среднего, рассчитанного по выборке размера из генеральной совокупности. Величина ошибки SDx̅ зависит от дисперсии генеральной совокупности и объёма выборки и рассчитывается по формуле:

SDx̅ = σ / √ n, где σ — величина стандартного разброса генеральной совокупности, а n — объём выборки.

Статистическая закономерность — это количественная форма проявления причинной связи. Она возникает как результат воздействия большого числа причин, действующих либо постоянно, либо только временами. Существует ряд статистических критериев, которые позволяют сравнивать экспериментально полученное распределение с нормальным, полученным в теории. Погрешность измерения — отклонение измеренного значения величины от действительного, являющиеся характеристикой точности измерения. Вместе с полученным результатом должна указываться погрешность измерений.

Определение понятия

Точность определения – это максимальное отклонение результата, который получен от всех измеренных величин одной и той же поворотной точки. Еще точностью называют случайный разброс ошибок около их средней величины. Это одно и то же, и чем больше проведено измерений, тем меньше вероятности допустить неточность при конечном расчете. Большое количество замеров — это не прихоть геодезиста, а необходимое уточнение.

Чтобы определить точность определения, рассчитывают среднюю квадратическую погрешность. Она будет принята равной величине средней погрешности той характерной точки, которая имеет максимальное значение. Координаты этих точек контура устанавливаются с точностью определения координат тех точек границ территории, где расположены такие объекты, как:

• здание;
• сооружение;
• незаконченная постройка.

Как определяются границы земельного участка?

Любой земельный участок в геодезии рассматривается в качестве плоской геометрической фигуры определённой формы, а границей считается совокупность всех линий, которые и составляют эту фигуру. Для определения фактической границы проводится геодезическое межевание. Сколько по времени делается межевание земельного участка узнайте тут. Во время межевания кадастровый инженер определяет географические координаты так называемых узловых точек, соединив которые прямыми линиями можно получить границы участка.

• Если участок имеет прямоугольную форму, а какие-либо дефекты рельефа отсутствуют, то в таком случае достаточно определить координаты вершин прямоугольника, которые и будут являться узловыми точками.
• Если же участок имеет вид сложной геометрической фигуры и/или имеются дефекты рельефа, то тогда вводятся дополнительные узловые точки, которые будут более точно определять границы.

Границы земельного участка могут определяться исключительно кадастровым инженером. Видео того, как делается межевание земельного участка прямо здесь.

В качестве такого работника могут выступать следующие лица:

1. Государственные инженеры, которые прошли соответствующую подготовку и числятся в штате соответствующей государственной организации.
2. Сотрудники частных организаций, у которых есть государственная лицензия на ведение подобной деятельности.
3. Частные инженеры-предприниматели, которые прошли подготовку и имеют государственную лицензию.

После межевания в Кадастровый реестр вносятся сведения о координатах узловых точек. Стоимость постановки земельного участка на кадастровый учёт в этой статье. Если у хозяина земли появились сомнения по поводу достоверности границ, то он может обратиться в Кадастровые органы для проведения повторного межевания, а в случае обнаружения кадастровых ошибок информация о координатах может быть пересмотрена. Мы уже написали подробно о том, можно ли изменить границы земельного участка после межевания в отдельной статье.

Межевание рекомендуется сделать в том случае, если оно ещё ни разу не проводилось, например, если участок вам достался по наследству, поскольку в противном случае имущественные права хозяина будут сильно ограничены. Эту территорию нельзя продать, сдать в аренду, подарить или завещать.

Возникла проблема? Позвоните юристу:

Москва и Московская область (звонок бесплатен) Санкт-Петербург и Лен.область

От чего зависит точность определения координат при межевании?

Точность определения координат зависит от следующих факторов:

1. Квалификация инженера и методика измерения. Для подсчёта результатов могут использоваться разные методики, каждая из которых имеет свою плюсы и минусы. Также нужно учитывать человеческий фактор, поскольку на практике встречаются ситуации, когда кадастровые ошибки появляются из-за недобросовестности инженеров-геодезистов.
2. Точность измерительных приборов. Сегодня для измерения координат применяются GPS-навигаторы, а также различные геодезические приборы для оценки формы рельефа. Некоторые приборы (например, старые навигаторы) несколько отстают от современных, что может привести к появлению ошибки.
3. Внешние факторы. На точность могут оказать влияния и некоторые другие факторы — неблагоприятные погодные условия, температура воздуха, неровность рельефа и так далее.

Практическое применение

На практике среднеквадратическое отклонение позволяет оценить, насколько значения из множества могут отличаться от среднего значения.

Экономика и финансы

Среднее квадратическое отклонение доходности портфеля σ = D >>

В техническом анализе среднеквадратическое отклонение используется для построения линий Боллинджера, расчёта волатильности.

Климат

Предположим, существуют два города с одинаковой средней максимальной дневной температурой, но один расположен на побережье, а другой внутри континента. Известно, что в городах, расположенных на побережье, множество различных максимальных дневных температур меньше, чем у городов, расположенных внутри континента. Поэтому среднеквадратическое отклонение максимальных дневных температур у прибрежного города будет меньше, чем у второго города, несмотря на то, что среднее значение этой величины у них одинаковое, что на практике означает, что вероятность того, что максимальная температура воздуха каждого конкретного дня в году будет сильнее отличаться от среднего значения, выше у города, расположенного внутри континента.

Спорт

Предположим, что есть несколько футбольных команд, которые оцениваются по некоторому набору параметров, например, количеству забитых и пропущенных голов, голевых моментов и т. п. Наиболее вероятно, что лучшая в этой группе команда будет иметь лучшие значения по большему количеству параметров. Чем меньше у команды среднеквадратическое отклонение по каждому из представленных параметров, тем предсказуемее является результат команды, такие команды являются сбалансированными. С другой стороны, у команды с большим значением среднеквадратического отклонения сложно предсказать результат, что в свою очередь объясняется дисбалансом, например, сильной защитой, но слабым нападением.

Использование среднеквадратического отклонения параметров команды позволяет в той или иной мере предсказать результат матча двух команд, оценивая сильные и слабые стороны команд, а значит, и выбираемых способов борьбы.

Основные сведения

Среднеквадратическое отклонение определяется как квадратный корень из дисперсии случайной величины: σ = D >>

Среднеквадратическое отклонение измеряется в единицах измерения самой случайной величины и используется при расчёте стандартной ошибки среднего арифметического, при построении доверительных интервалов, при статистической проверке гипотез, при измерении линейной взаимосвязи между случайными величинами.

На практике, когда вместо точного распределения случайной величины в распоряжении имеется лишь выборка, стандартное отклонение, как и математическое ожидание, оценивают (выборочная дисперсия), и делать это можно разными способами. Термины «стандартное отклонение» и «среднеквадратическое отклонение» обычно применяют к квадратному корню из дисперсии случайной величины (определённому через её истинное распределение), но иногда и к различным вариантам оценки этой величины на основании выборки.

В частности, если x i >

i

x ¯ = 1 n ∑ i = 1 n x i = 1 n ( x 1 + … + x n ) , >=>\sum _^x_=>(x_+\ldots +x_),>

то два основных способа оценки стандартного отклонения записываются нижеследующим образом.

Оценка стандартного отклонения на основании смещённой оценки дисперсии (иногда называемой просто выборочной дисперсией ):

S = 1 n ∑ i = 1 n ( x i − x ¯ ) 2 . >\sum _^\left(x_—>\right)^>>.>

Это в буквальном смысле среднее квадратическое разностей измеренных значений и среднего.

Оценка стандартного отклонения на основании несмещённой оценки дисперсии (подправленной выборочной дисперсии , в ГОСТ Р 8.736-2011 — «среднее квадратическое отклонение»):

S 0 = n n − 1 S 2 = 1 n − 1 ∑ i = 1 n ( x i − x ¯ ) 2 . =>S^>>=>\sum _^\left(x_—>\right)^>>.>

Само по себе, однако, S 0 >

Кроме того, среднеквадратическим отклонением называют математическое ожидание квадрата разности истинного значения случайной величины и её оценки для некоторого метода оценки . Если оценка несмещённая (выборочное среднее — как раз несмещённая оценка для случайной величины), то эта величина равна дисперсии этой оценки.

Формула, примеры решения задач

Для четырех измеренных значений величины b формула среднеквадратичного отклонения будет выглядеть следующим образом:

\(\sigma=\sqrt{\frac{\triangle b_1+\triangle b_2+\triangle b_3+\triangle b_4}4}\)

где Db₁ — Db₄ являются абсолютными погрешностями каждой исследуемой величины.

Рассмотрим пример решения конкретной задачи.

Задача

При проведении лабораторной работы по физике школьники несколько раз измерили напряжение электрического тока и получили следующие значения:

\(U_1=4.22B\\U_2=4.30B\\U_3=4.27B\\U_4=4.23B\\U_5=4.20B\)

Необходимо рассчитать погрешности (абсолютные и относительные) каждого измерения, дисперсию и среднеквадратическое отклонение.

Решение

Определим среднее арифметическое значение напряжения в данной работе:

\(U_c=\sqrt{\frac{U_1+U_2+U_3+U_4+U_5}5}=\frac{4.22+4.30+4.27+4.23+4.20}5=4.244B\)

Теперь рассчитаем для каждого полученного измерения абсолютную и относительную погрешности. Так как абсолютная погрешность определяется как разница между средним арифметическим и полученным значением, то

\(\triangle U_1=0.024\\\triangle U_2=-0.056\\\triangle U_3=-0.026\\\triangle U_4=0.014\\\triangle U_5=0.044\)

Находим относительную погрешность:

\(\sigma_1=\frac{\left|U_1\right|}{U_c}\times100\%=0.50\%\\\sigma_2=\frac{\left|U_2\right|}{U_c}\times100\%=1.06\%\\\sigma_3=\frac{\left|U_3\right|}{U_c}\times100\%=0.50\%\\\sigma_4=\frac{\left|U_4\right|}{U_c}\times100\%=0.25\%\\\sigma_5=\frac{\left|U_5\right|}{U_c}\times100\%=0.84\%\\\)

Зная абсолютные погрешности несложно вычислить дисперсию:

\(D=\frac{\triangle U_1^2+{\triangle U_2}^2+{\triangle U_3}^2+{\triangle U_4}^2+{\triangle U_5}^2}5=0.001304\\\)

Теперь можно вычислить среднеквадратичное отклонение:

Расчет среднеквадратичного (стандартного) отклонения

Формулы вычисления стандартного отклонения

Разница между формулами S и σ («n» и «n–1»)

Состоит в том, что мы анализируем — всю выборку или только её часть:

• только её часть – используется формула S (с «n–1»),
• полностью все данные – используется формула σ (с «n»).

Как рассчитать стандартное отклонение?

Пример 1 (с σ)

Рассмотрим данные о запасе какого-то товара на складах Предприятия Б.

День 1	День 2	День 3	День 4
Пред.Б	15	26	15	24

Если значений выборки немного (небольшое n, здесь он равен 4) и анализируются все значения, то применяется эта формула:

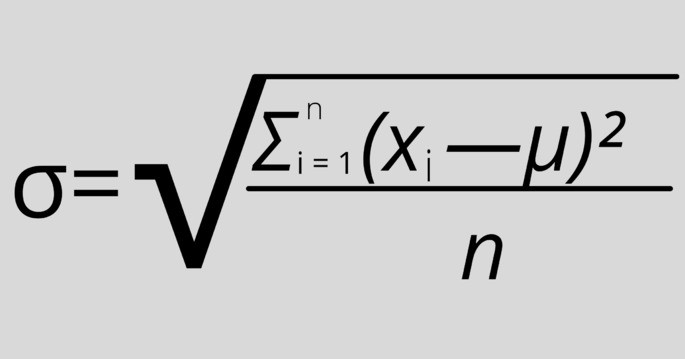
Применяем эти шаги:

1. Найти среднее арифметическое выборки:

μ = (15 + 26 + 15+ 24) / 4 = 20

2. От каждого значения выборки отнять среднее арифметическое:

x1 — μ = 15 — 20 = -5

x2 — μ = 26 — 20 = 6

x3 — μ = 15 — 20 = -5

x4 — μ = 24 — 20 = 4

3. Каждую полученную разницу возвести в квадрат:

4. Сделать сумму полученных значений:

Σ (xi — μ)² = 25 + 36+ 25+ 16 = 102

5. Поделить на размер выборки (т.е. на n):

(Σ (xi — μ)²)/n = 102 / 4 = 25,5

6. Найти квадратный корень:

√((Σ (xi — μ)²)/n) = √ 25,5 ≈ 5,0498

Пример 2 (с S)

Задача усложняется, когда существуют сотни, тысячи или даже миллионы данных. В этом случае берётся только часть этих данных и анализируется методом выборки.

У Андрея 20 яблонь, но он посчитал яблоки только на 6 из них.

Популяция — это все 20 яблонь, а выборка — 6 яблонь, это деревья, которые Андрей посчитал.

Яблоня 1	Яблоня 2	Яблоня 3	Яблоня 4	Яблоня 5	Яблоня 6
9	2	5	4	12	7

Так как мы используем только выборку в качестве оценки всей популяции, то нужно применить эту формулу:

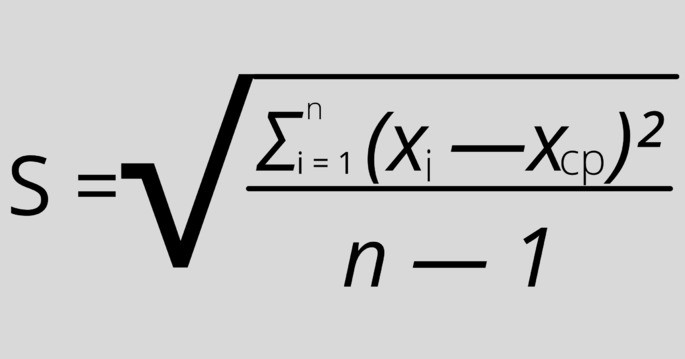
Математически она отличается от предыдущей формулы только тем, что от n нужно будет вычесть 1. Формально нужно будет также вместо μ (среднее арифметическое) написать X ср.

Применяем практически те же шаги:

1. Найти среднее арифметическое выборки:

Xср = (9 + 2 + 5 + 4 + 12 + 7) / 6 = 39 / 6 = 6,5

2. От каждого значения выборки отнять среднее арифметическое:

X1 – Xср = 9 – 6,5 = 2,5

X2 – Xср = 2 – 6,5 = –4,5

X3 – Xср = 5 – 6,5 = –1,5

X4 – Xср = 4 – 6,5 = –2,5

X5 – Xср = 12 – 6,5 = 5,5

X6 – Xср = 7 – 6,5 = 0,5

3. Каждую полученную разницу возвести в квадрат:

(X1 – Xср)² = (2,5)² = 6,25

(X2 – Xср)² = (–4,5)² = 20,25

(X3 – Xср)² = (–1,5)² = 2,25

(X4 – Xср)² = (–2,5)² = 6,25

(X5 – Xср)² = 5,5² = 30,25

(X6 – Xср)² = 0,5² = 0,25

4. Сделать сумму полученных значений:

Σ (Xi – Xср)² = 6,25 + 20,25+ 2,25+ 6,25 + 30,25 + 0,25 = 65,5

5. Поделить на размер выборки, вычитав перед этим 1 (т.е. на n–1):

(Σ (Xi – Xср)²)/(n-1) = 65,5 / (6 – 1) = 13,1

6. Найти квадратный корень:

S = √((Σ (Xi – Xср)²)/(n–1)) = √ 13,1 ≈ 3,6193

Среднеквадратичная погрешность

В заключение следует определить среднеквадратичную погрешность на выходе идеального фильтра нижних частот.
 

Заметим, что определить среднеквадратичную погрешность отдельных составляющих не всегда просто. В ряде случаев необходимо ознакомиться с технологией изготовления комплектующих изделий и методикой присвоения им погрешностей с тем, чтобы обеспечить одинаковый подход при определении погрешности отдельных составляющих. Так, при изготовлении образцовых сопротивлений, последние группируются по значениям предельных погрешностей ( 6 -) — Если известен закон распределения погрешности внутри группы сопротивлений, то нетрудно определить значение среднеквадратичной погрешности.
 

Характеристика насоса IL-11 при перекачке жидкостей с вязкостью ( в Ст.

Сопоставление коэффициентов ассоциации со среднеквадратичной погрешностью показало, что только для первых четырех признаков, перечисленных в табл. 110, связь их с определением типа месторождения, не является случайной. Эти признаки и была взяты для дальнейшего исследования.
 

Мера погрешности (2.26) называется среднеквадратичной погрешностью реализации.
 

Проследим теперь, как преобразуются среднеквадратичные погрешности при производстве математических операций. Величины, над которыми производятся операции, будем предполагать независимыми в том смысле, как это указывалось ранее.
 

Числа в круглых скобках представляют собой среднеквадратичные погрешности в последних цифрах.
 

В табл. 2 приведены значения среднеквадратичных погрешностей аппроксимации полос S, для различных вариантов нумерации пер: Вых линий ветвей Р, RI и Qb Рядом приведены значения среднеквадратичных погрешностей 5, полученных при аппроксимации каждой ветви в отдельности.
 

Из последнего примера следует, что среднеквадратичная погрешность эмпирической формулы, полученная без учета доверительных пределов, может быть значительно ниже, чем та, которая должна быть названа как погрешность формулы при достаточно высоком уровне доверия к результату.
 

Из последней леммы следует, что чем меньше среднеквадратичная погрешность, тем меньше рассеяние значений случайной величины около ее математического ожидания.
 

Коэффициент корреляции и уравнения регрессии для физико-механических показателей резиновых смесей и готовых протекторов.

Для определения достоверности найденной корреляционной зависимости вычислялись среднеквадратичная погрешность коэффициентов корреляции оог и отношение г 1аог, которое не должно быть менее 2 6, если зависимость достоверна. Таким образом, для уточнения технических условий на физико-механические показатели резиновых смесей следует задаться физико-механическими показателями готовой продукции, а по уравнениям регрессии вычислить аналогичные показатели резиновых смесей. Так, найденная корреляционная — зависимость позволяет повысить точность и надежность определения показателей качества продукции без дополнительных затрат.
 

Надежность полученных значений 0 характеризуется соответствующим значением среднеквадратичной погрешности, а также степенью представленности данного заместителя ( фактора) во всей совокупности установочных серий, выражаемой дробью, числитель которой равен числу серий, в которых этот заместитель ( фактор) представлен, а знаменатель равняется общему числу серий.
 

Эти величины и использованы для получения оценки среднеквадратичной погрешности.
 

Корень квадратный из этой величины носит название среднеквадратичной погрешности измерения.
 

4.5. Заключение к главе «Измерительные каналы»

В зависимости от цели исследований или измерений необходимо
различать такие характеристики измерительных каналов, как разрешающая
способность, порог чувствительности, динамический диапазон или точность.

Усреднение результатов многократных измерений возможно
только при большой случайной составляющей погрешности и практически редко дает
повышение точности более чем в 2…3 раза. Однако это не относится к
разрешающей способности, которая может быт увеличена существенно.

Нельзя игнорировать динамическую погрешность измерений,
которая обычно не указывается в эксплуатационной документации. Отсутствие
информации о ее величине не свидетельствует об отсутствии самой погрешности.

При выборе частоты дискретизации аналогового сигнала перед
измерениями с максимальной частотой, допускаемой модулем ввода, необходимо
убедиться, что спектр помехи лежит ниже половины частоты дискретизации или
использовать дополнительно антиалиасный фильтр.

Ошибки, допущенные на этапе проектирования и монтажа
автоматизированной системы, могут сделать измерения недостоверными.

При нахождении итоговой погрешности измерений следует
различать детерминированные, случайные и коррелированные погрешности, которые
суммируются по-разному.

Одним из путей упрощения методики расчета погрешностей может
быть использование средств измерений с большой избыточностью по точности. Тогда
учет тонких нюансов теории погрешностей становится излишним.

Обзор литературы

В работе []
рассмотрено соотношение между доверительным интервалом и доверительной
вероятностью для случая очень ограниченной исходной информации, при малом числе
измерений и унимодальной плотности распределения; в
[]
найдена оценка математического ожидания и
дисперсии погрешности при косвенных измерениях со случайной коррелированной
погрешностью, в том числе для нелинейных моделей измерения. Путем моделирования
методом Монте-Карло показано, что погрешность предложенного аналитического
метода оценки погрешности составляет около 0,5%. В работе
[]
предложен алгоритм усреднения результатов
многократных измерений для восстановления сигнала, подаваемого для измерения
сопротивления кожи человека. В
[]
разработан метод оценки класса точности средств
измерений по динамической погрешности независимо от формы измеряемого сигнала.
В статьях
исследованы методы коррекции динамической погрешности, позволяющие снизить
динамическую погрешность измерительных преобразователей и датчиков.
В []
предлагается вместо аналитического метода расчета случайной
составляющей погрешности в автоматизированных системах измерений использовать
метод Монте-Карло. В серии
метрологических инструкций приводятся полезные для
практики сведения, касающиеся измерительных систем средств автоматизации.